Let x be the smallest positive integer such that when 14 divides , the remainder is 7, and when 15 divides x, the remainder is 5. Which one of the following is correct ?
20<x<30
30<x<40
40<x<50
x>50
To solve the problem, we need to find the smallest positive integer x such that:
1. When x is divided by 14, the remainder is 7.
2. When x is divided by 15, the remainder is 5.
Let's break down the steps to find x.
Step 1: Set up the equations based on the remainders.
From the first condition:
- When x is divided by 14 and the remainder is 7, we can express this as:
x=14k+7
where k is a non-negative integer.
From the second condition:
- When x is divided by 15 and the remainder is 5, we can express this as:
x=15m+5
where m is also a non-negative integer.
Step 2: Equate the two expressions for x.
Now we have two expressions for x:
14k+7=15m+5
Step 3: Rearrange the equation.
Rearranging gives:
14k−15m=−2
Step 4: Solve for integers k and m.
We can rearrange it to:
14k=15m−2
This means 15m−2 must be divisible by 14.
Step 5: Find values of m.
We can test values of m to find the smallest positive integer k:
- For m=0:
15(0)−2=−2(not valid)
- For m=1:
15(1)−2=13(not divisible by 14)
- For m=2:
15(2)−2=28(divisible by 14, gives k=2)
- For m=3:
15(3)−2=43(not divisible by 14)
- For m=4:
15(4)−2=58(not divisible by 14)
- For m=5:
15(5)−2=73(not divisible by 14)
- For m=6:
15(6)−2=88(divisible by 14, gives k=6)
Step 6: Calculate x.
Using m=2 and k=2:
x=15(2)+5=30+5=35
or
x=14(2)+7=28+7=35
Conclusion
The smallest positive integer x that satisfies both conditions is 35.
2. When x is divided by 15, the remainder is 5.
- When x is divided by 14 and the remainder is 7, we can express this as:
x=14k+7
where k is a non-negative integer.
- When x is divided by 15 and the remainder is 5, we can express this as:
x=15m+5
where m is also a non-negative integer.
14k+7=15m+5
14k−15m=−2
14k=15m−2
This means 15m−2 must be divisible by 14.
- For m=0:
15(0)−2=−2(not valid)
- For m=1:
15(1)−2=13(not divisible by 14)
- For m=2:
15(2)−2=28(divisible by 14, gives k=2)
- For m=3:
15(3)−2=43(not divisible by 14)
- For m=4:
15(4)−2=58(not divisible by 14)
- For m=5:
15(5)−2=73(not divisible by 14)
- For m=6:
15(6)−2=88(divisible by 14, gives k=6)
x=15(2)+5=30+5=35
or
x=14(2)+7=28+7=35
Similar Questions
Knowledge Check
When an integer K is divided by 3, the remainder is 1, and when K+ 1 is divided by 5, the remainder is 0. Of the following, a possible value of K is
A62B63C64D65When an integer K is divided by 3, the remainder is 1, and when K+ 1 is divided by 5, the remainder is 0. Of the following, a possible value of K is
A62B63C64D65Find the remainder when 1315 is divided by 5.
A4B3C2D1
Find the remainder when x15 is divided by x−2
View SolutionWhen the positive integer n is divided by 7 ,the remainder is 2 .What is the remainder when 5n is divided by 7?
View SolutionA positive integer when divided by 425 gives a remainder 45.When the same number is divided by 17, the remainder will be
View SolutionWhen
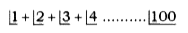 , is divided by 5, the remainder obtained is ?
, is divided by 5, the remainder obtained is ?
View SolutionA positive integer when divided by 425 gives a remainder 45. When the same number is divided by 17, the remainder will be
View Solution
