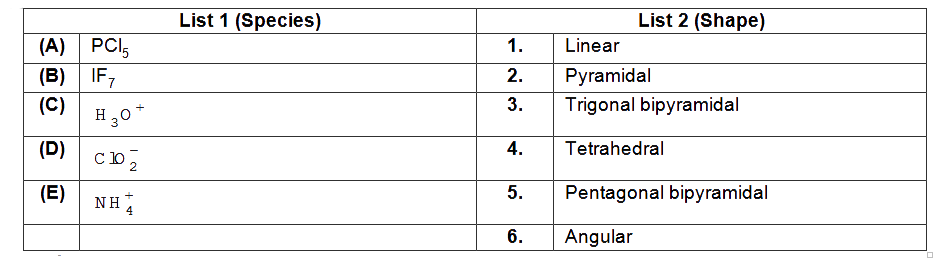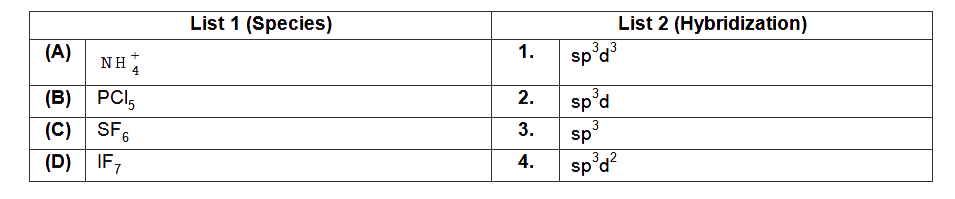If radius of a sphere is rational, then which of the following is/are correct ?
1. Its surface area is rational.
2. Its volume is rational.
Select the correct answer using the code given below :
1 only
2 only
Both 1 and 2
Neither 1 nor 2
To solve the problem, we need to analyze the statements regarding the surface area and volume of a sphere when the radius is a rational number.
1. Understand the formulas:
- The surface area A of a sphere is given by the formula:
A=4πr2
- The volume V of a sphere is given by the formula:
V=43πr3
2. Identify the nature of the radius:
- We are given that the radius r is a rational number. A rational number can be expressed as the quotient of two integers (e.g., ab where a and b are integers and b≠0).
3. Evaluate the surface area:
- Substitute the rational radius r into the surface area formula:
A=4πr2
- Here, r2 is also rational (since the square of a rational number is rational).
- However, π is an irrational number. The product of a rational number (4 and r2) and an irrational number (π) is irrational.
- Therefore, the surface area A is irrational.
4. Evaluate the volume:
- Substitute the rational radius r into the volume formula:
V=43πr3
- Again, r3 is rational (since the cube of a rational number is rational).
- The fraction 43 is also rational. Thus, the product of two rational numbers (43 and r3) multiplied by the irrational number π results in an irrational number.
- Therefore, the volume V is also irrational.
5. Conclusion:
- Since both the surface area and volume of the sphere are irrational when the radius is rational, we conclude that:
- Statement 1 (Surface area is rational) is incorrect.
- Statement 2 (Volume is rational) is incorrect.
- Thus, the correct answer is that neither statement 1 nor statement 2 is correct.
Final Answer:
The correct option is D (neither 1 nor 2 are correct).
- The surface area A of a sphere is given by the formula:
A=4πr2
- The volume V of a sphere is given by the formula:
V=43πr3
- We are given that the radius r is a rational number. A rational number can be expressed as the quotient of two integers (e.g., ab where a and b are integers and b≠0).
- Substitute the rational radius r into the surface area formula:
A=4πr2
- Here, r2 is also rational (since the square of a rational number is rational).
- However, π is an irrational number. The product of a rational number (4 and r2) and an irrational number (π) is irrational.
- Therefore, the surface area A is irrational.
- Substitute the rational radius r into the volume formula:
V=43πr3
- Again, r3 is rational (since the cube of a rational number is rational).
- The fraction 43 is also rational. Thus, the product of two rational numbers (43 and r3) multiplied by the irrational number π results in an irrational number.
- Therefore, the volume V is also irrational.
- Since both the surface area and volume of the sphere are irrational when the radius is rational, we conclude that:
- Statement 1 (Surface area is rational) is incorrect.
- Statement 2 (Volume is rational) is incorrect.
- Thus, the correct answer is that neither statement 1 nor statement 2 is correct.
The correct option is D (neither 1 nor 2 are correct).
Similar Questions
Knowledge Check
Select the correct answer using the codes given below :
A1,2 and 4B1,3 and 4C2 and 3D1 and 4.Match 1list I with list II and select the correct answer using the code given below
 A1.c,2. b,3.d ,4.eB1. a,2. c, 3. b, 4.dC1. d, 2. a, 3. b , 4. dD1. e,2. b,3. c,4. d
A1.c,2. b,3.d ,4.eB1. a,2. c, 3. b, 4.dC1. d, 2. a, 3. b , 4. dD1. e,2. b,3. c,4. dMatch list - 1 with ist -- Il and select the correct answer using the codes given below.
 A3412B3142C3421D4321
A3412B3142C3421D4321
Match List 1 with List 2. Select the correct answer using the codes given below the list.
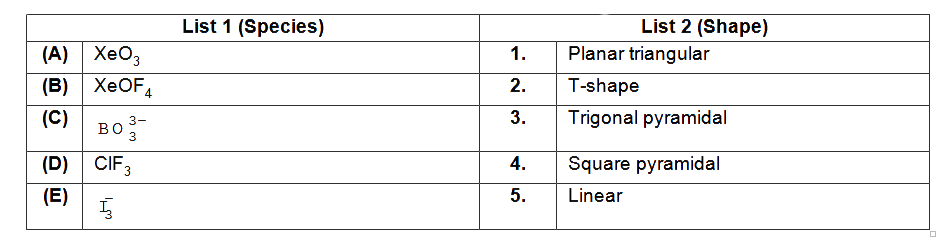
View SolutionMatch List I with List II and select the correct answer using the codes given below :

Codes
View SolutionMatch list - 1 with ist -- Il and select the correct answer using the codes given below.

View SolutionMatch the following and select the correct answer by using codes given below.
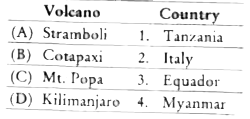
View SolutionMatch Column I with Column II and select the correct answer using the codes given below :

Answer codes:
View Solution