ABCD is a cyclic quadrilateral. The bisectors of the angles A, B, C and D. cut the circle at P, Q, R and S respectively. What is ∠PQR+∠RSP equal to ?
90∘
135∘
180∘
270∘
To solve the problem, we need to find the sum of the angles ∠PQR and ∠RSP in the cyclic quadrilateral ABCD where the angle bisectors intersect the circumcircle at points P,Q,R, and S.
1. Understanding the Cyclic Quadrilateral:
- A cyclic quadrilateral is a four-sided figure where all vertices lie on a single circle. The opposite angles of a cyclic quadrilateral sum up to 180∘.
2. Identifying the Angles:
- The angle bisectors of angles A,B,C, and D intersect the circumcircle at points P,Q,R, and S respectively.
- Therefore, P is on the angle bisector of A, Q is on the angle bisector of B, R is on the angle bisector of C, and S is on the angle bisector of D.
3. Using Properties of Cyclic Quadrilaterals:
- By the property of cyclic quadrilaterals, the sum of the angles ∠PQR and ∠RSP can be determined.
- The angles ∠PQR and ∠RSP are formed by the intersection of the lines from points P and R to points Q and S.
4. Applying the Angle Sum Property:
- Since P,Q,R,S are points on the circumcircle of the cyclic quadrilateral, we can apply the property that states:
∠PQR+∠RSP=180∘
5. Conclusion:
- Therefore, the sum of the angles ∠PQR and ∠RSP is equal to 180∘.
Final Answer:
∠PQR+∠RSP=180∘
- A cyclic quadrilateral is a four-sided figure where all vertices lie on a single circle. The opposite angles of a cyclic quadrilateral sum up to 180∘.
- The angle bisectors of angles A,B,C, and D intersect the circumcircle at points P,Q,R, and S respectively.
- Therefore, P is on the angle bisector of A, Q is on the angle bisector of B, R is on the angle bisector of C, and S is on the angle bisector of D.
- By the property of cyclic quadrilaterals, the sum of the angles ∠PQR and ∠RSP can be determined.
- The angles ∠PQR and ∠RSP are formed by the intersection of the lines from points P and R to points Q and S.
- Since P,Q,R,S are points on the circumcircle of the cyclic quadrilateral, we can apply the property that states:
∠PQR+∠RSP=180∘
- Therefore, the sum of the angles ∠PQR and ∠RSP is equal to 180∘.
∠PQR+∠RSP=180∘
Similar Questions
Knowledge Check
ABC is a cyclic triangle and the bisectors of ∠BAC,∠ABCand∠BCA meet the circle at P,Q and R respectively. Then the angle ∠RQP is:
A90∘−∠B2B90∘+∠B2C90∘+∠C2D90∘+∠B2ABC is a cyclic triangle and the bisectors of ∠BAC,∠ABCand∠BCA meet the circle at P,Q and R respectively. Then the angle ∠RQP is:
A90∘−B2B90∘+B2C90∘+C2D90∘−A2ABCD is a quadrilateral inscribed in a circle (radius=r). The bisectors of the angles DAB and BCD intersect the circle at X and Y. respectively. What is the length of the straight line XY?
Aπr2B2rC(r+2)Dπr22
Ina cyclic quadrilateral
∠A+∠C=∠B+∠D=?
View SolutionIf ABCD is a cyclic quadrilateral, then cosA+cosB is equal to
View SolutionA triangle ABC is inscribed in a circle and the bisectors of the angles A, B and C meet the cir cumference at P, Q and R respec tively. The angles of the triangle PQR respectively are
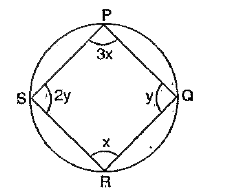
View SolutionPQRs is a cyclic quadrilateral. Find the measure of ∠Pand∠Q.
View SolutionIf the bisector of the angles A and B of a quadrilateral ABCD meet at O, then ∠AOB is equal to:
View Solution
