In the figure , L is the centre of the circle, and ML is the perpendicular to LN. If the area of the triangel MLN is 36 then the area of the circle is:
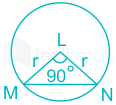
68π
66π
70π
72π
The correct Answer is:D
To solve the problem step by step, we will use the information given about the triangle MLN and the relationship between the triangle and the circle.
Step 1: Understand the triangle and its area
Given that the area of triangle MLN is 36, we can use the formula for the area of a triangle:
Area=12×base×height
Step 2: Identify the base and height
In triangle MLN, we can consider:
- ML as the height (since ML is perpendicular to LN)
- LN as the base
Let the length of LN be b and the length of ML be h. Therefore, we can write:
12×b×h=36
Step 3: Solve for b×h
Multiplying both sides by 2, we get:
b×h=72
Step 4: Relate the triangle to the circle
Since L is the center of the circle and ML is the height from M to LN, the length ML represents the radius of the circle (let's denote it as r). Thus, we can express the area of the circle using the formula:
Area of the circle=πr2
Step 5: Find the relationship between r, b, and h
From the right triangle MLN, we can use the Pythagorean theorem:
LN2=ML2+MN2
This means that:
b2=r2+MN2
However, we do not have enough information to find b and MN directly. Instead, we can use the area of the triangle to express r.
Step 6: Express r in terms of the area
Since we have b×h=72 and h=r, we can express b as:
b=72r
Step 7: Substitute b into the area of the circle formula
Now, we can express the area of the circle in terms of r:
Area of the circle=πr2
Step 8: Calculate the area of the circle
Since we know that the area of triangle MLN is 36, and we have established the relationship, we can conclude that the radius r is related to the area of the triangle.
To find the area of the circle, we can assume a radius that satisfies the area condition. Since we have b×h=72 and h=r, we can find r using the area of the triangle:
Area of the circle=πr2=π(72b)2
However, since we do not have a specific value for b, we can conclude that the area of the circle is directly related to the area of the triangle, and we can assume a standard radius based on the area given.
Final Calculation
Assuming r=12 (since 36=12×12×12), we can calculate the area of the circle:
Area of the circle=π(12)2=144π
Conclusion
Thus, the area of the circle is:
Area of the circle=144π
Given that the area of triangle MLN is 36, we can use the formula for the area of a triangle:
Area=12×base×height
In triangle MLN, we can consider:
- ML as the height (since ML is perpendicular to LN)
- LN as the base
12×b×h=36
Multiplying both sides by 2, we get:
b×h=72
Since L is the center of the circle and ML is the height from M to LN, the length ML represents the radius of the circle (let's denote it as r). Thus, we can express the area of the circle using the formula:
Area of the circle=πr2
From the right triangle MLN, we can use the Pythagorean theorem:
LN2=ML2+MN2
This means that:
b2=r2+MN2
Since we have b×h=72 and h=r, we can express b as:
b=72r
Now, we can express the area of the circle in terms of r:
Area of the circle=πr2
Since we know that the area of triangle MLN is 36, and we have established the relationship, we can conclude that the radius r is related to the area of the triangle.
Area of the circle=πr2=π(72b)2
Assuming r=12 (since 36=12×12×12), we can calculate the area of the circle:
Area of the circle=π(12)2=144π
Thus, the area of the circle is:
Area of the circle=144π
Similar Questions
In the figure, L is the centre of the circle, and ML is the perpendicular to LN. If the area of the triangle MLN is 36, then the area of the circle is:
इस आकृति में, L वृत्त का केंद्र है तथा ML, LN पर ल है। लम्ब है। यदि त्रिभुज MLN का क्षेत्रफल 36 है, तो इस वृत्त का क्षेत्रफल ज्ञात कीजिए।
View SolutionIf the following figure, O is the centre of the circle and XO is perpendicular to OY. If the area of the triangle XOY is 32, then the area of the circle is :

View Solution
Knowledge Check
In the adjoining figure ABC is an equilateral triangle and C is the centre of the circle, A and B lie on the circle. What is the area of the shaded region , if the diameter of the circle is 28 cm ?
 A(10223−49√3)cm2B(10323−98√3)cm2C(109−38√3)cmDnone of the above
A(10223−49√3)cm2B(10323−98√3)cm2C(109−38√3)cmDnone of the aboveIn the given figure, P is the centre of the circle. The area of the figure is
 A3256cm2B2492cm2C2942cm2D3256cm2
A3256cm2B2492cm2C2942cm2D3256cm2In the given figure, G, a point on the circle, is the centroid of the triangle OAB.
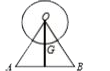
Find the ratio of the area of the equilateral triangle OAB to that of the circle whose centre is O.A7√3:44B21√3:88C7√3:88D21√3:44
In the given figure, O is the centre of the circle with radius 14 cm. Find the area of the shared portion

View SolutionIn the following figure, if O is the centre of the circle and radius OA=14cm, then the area of the shaded portion is:
View SolutionIn the figure, if O is the centre of the circle, PQ is chord. ∠POQ=90∘ area of shaded region is 114cm2 find the radius of the circle
(π=3.14)
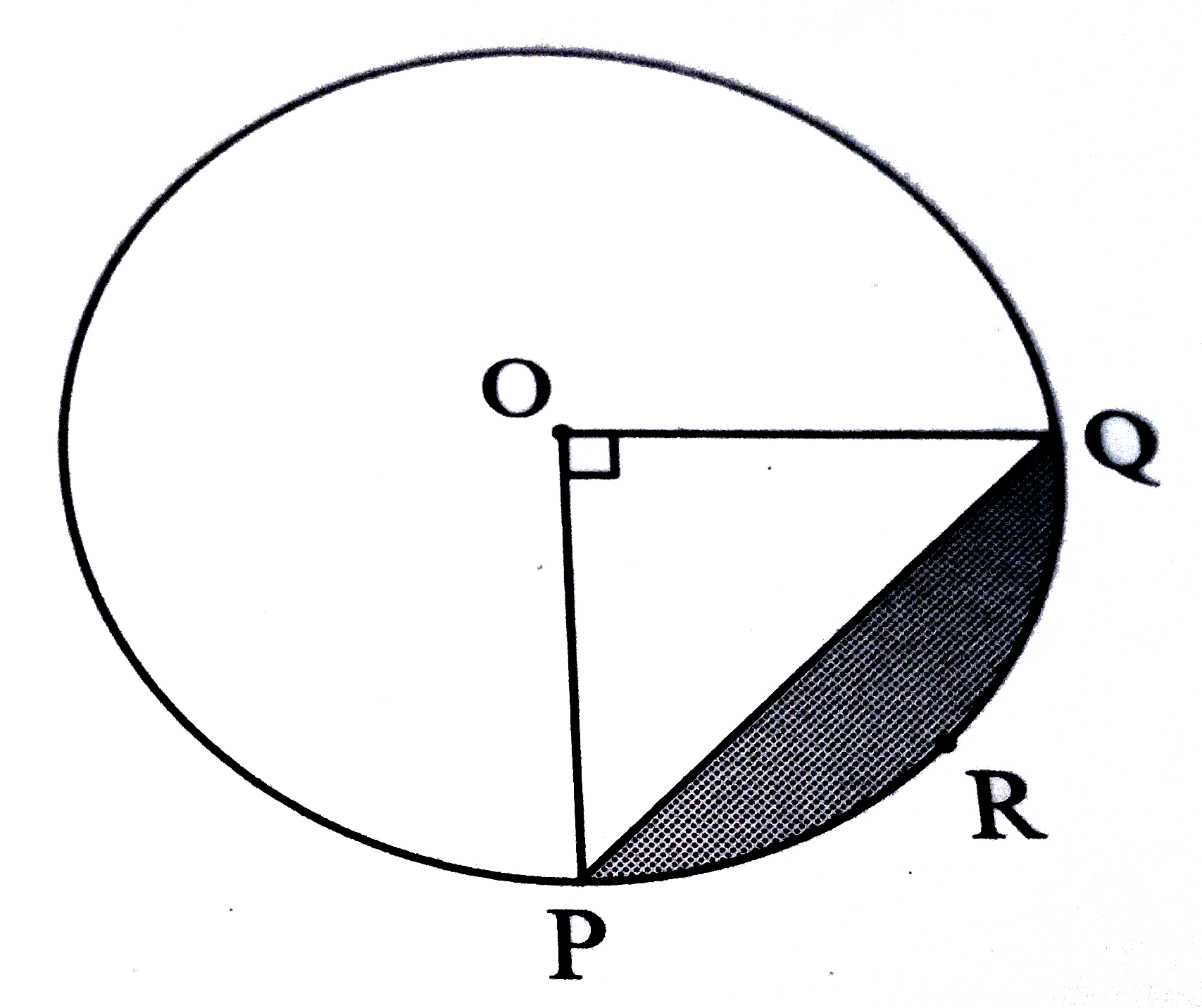
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
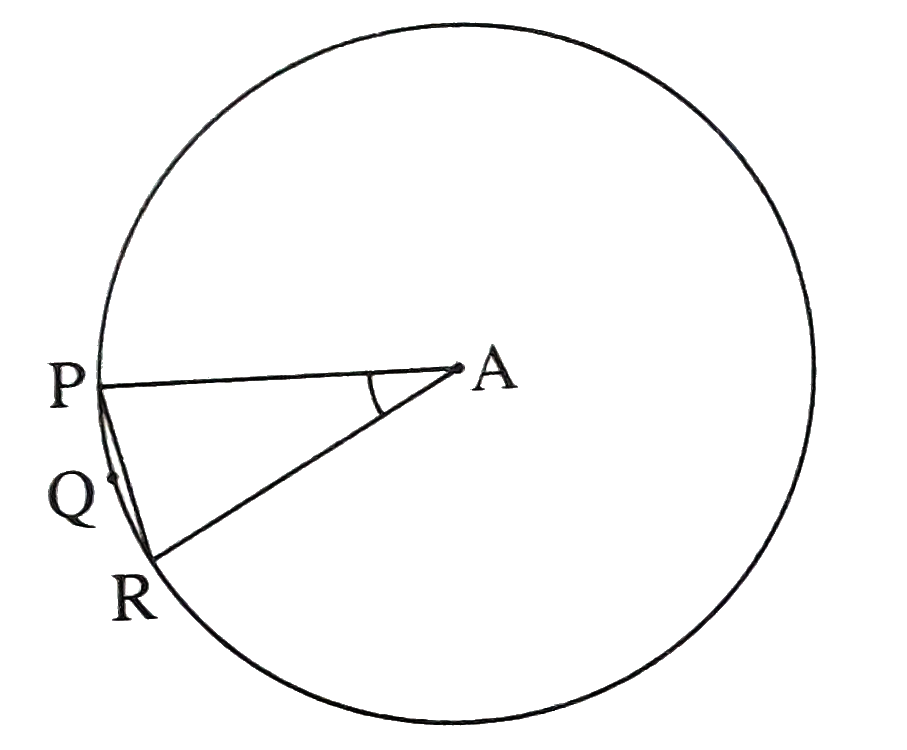
View SolutionIn the figure, if A is the centre of the circle. ∠PAR=30∘, AP=7.5,
find the area of the segment PQR. (π=3.14)
View Solution
