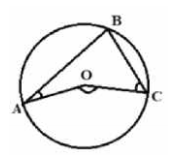
In the given figure, O is the centre of the circle. If ∠BAO=30∘ and ∠BCO=50∘ , then ∠AOC is equal to:

A
60∘
B
80∘
C
40∘
D
160∘
Video Solution
Text Solution
The correct Answer is:D
|
Answer
Step by step video, text & image solution for In the given figure, O is the centre of the circle. If angleBAO = 30^(@) and angleBCO = 50^(@) , then angleAOC is equal to: by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, O is the centre of the circle. ∠AOB=70∘, find ∠OCD :
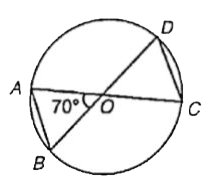 A70∘B55∘C65∘D110∘
A70∘B55∘C65∘D110∘ - Question 2 - Select One
In Fig, O is the center of the circle. Find the angle of △ABC.
 A130∘B150∘C135∘Dcan't be determined
A130∘B150∘C135∘Dcan't be determined - Question 3 - Select One
In the given figure, O is the centre of the circle and ∠ACB=25∘ Find ∠AOB
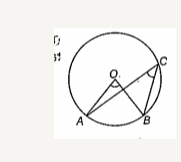 A25∘B50∘C75∘D60∘
A25∘B50∘C75∘D60∘
In the given figure, O is the centre of the circle∠AOB=90∘ Find m∠APB
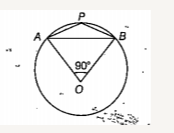 View Solution
View SolutionIn the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
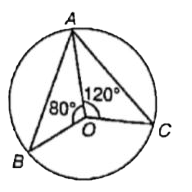 View Solution
View SolutionIn the given figure, O is the centre of the circle. The value of x is
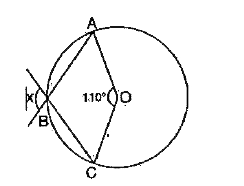 View Solution
View SolutionIn the given figure O is the centre of the circle and ∠CD=26∘, find ∠AOD :
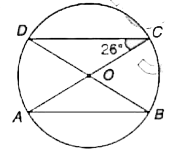 View Solution
View SolutionIn the given figure, O is the centre of circle, ∠AOB=100∘. Find ∠BCD :
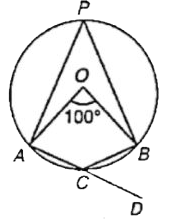 View Solution
View Solution