A particle 'A' disintegrates into other 'B' and then 'B' into 'C'. Find the graph suitable for number of atoms of B vs. time.
To solve the problem of finding the graph suitable for the number of atoms of B vs. time, we can follow these steps:
1. Understanding the Disintegration Process:
- We have a particle A that disintegrates into particle B.
- Particle B further disintegrates into particle C.
2. Initial Conditions:
- At time t=0:
- Number of atoms of A, NA(0)=N0 (maximum).
- Number of atoms of B, NB(0)=0.
- Number of atoms of C, NC(0)=0.
3. Decay of Particle A:
- The number of atoms of A at any time t can be expressed using the exponential decay formula:
NA(t)=N0e−λt
- Here, λ is the decay constant for A.
4. Formation of Particle B:
- As A decays, B is formed. The rate of change of B can be expressed as:
dNBdt=(rate of formation from A)−(rate of decay to C)
- The rate of formation from A is λNA(t) and the rate of decay to C is λ′NB(t) (where λ′ is the decay constant for B).
5. Differential Equation for B:
- Thus, we can write:
dNBdt=λNA(t)−λ′NB(t)
- Substituting NA(t):
dNBdt=λN0e−λt−λ′NB(t)
6. Behavior of B Over Time:
- Initially, at t=0, NB(0)=0.
- As time progresses, NB will increase due to the formation from A, but will eventually decrease as B decays into C.
7. Graph of Number of Atoms of B vs. Time:
- The graph will show an initial increase in the number of atoms of B as A decays, reaching a peak, and then a decrease as B decays into C.
- This results in a curve that rises to a maximum and then falls, resembling a typical exponential growth followed by decay.
Conclusion:
The suitable graph for the number of atoms of B vs. time is one that starts at zero, increases to a maximum, and then decreases over time.
- We have a particle A that disintegrates into particle B.
- Particle B further disintegrates into particle C.
- At time t=0:
- Number of atoms of A, NA(0)=N0 (maximum).
- Number of atoms of B, NB(0)=0.
- Number of atoms of C, NC(0)=0.
- The number of atoms of A at any time t can be expressed using the exponential decay formula:
NA(t)=N0e−λt
- Here, λ is the decay constant for A.
- As A decays, B is formed. The rate of change of B can be expressed as:
dNBdt=(rate of formation from A)−(rate of decay to C)
- The rate of formation from A is λNA(t) and the rate of decay to C is λ′NB(t) (where λ′ is the decay constant for B).
- Thus, we can write:
dNBdt=λNA(t)−λ′NB(t)
- Substituting NA(t):
dNBdt=λN0e−λt−λ′NB(t)
- Initially, at t=0, NB(0)=0.
- As time progresses, NB will increase due to the formation from A, but will eventually decrease as B decays into C.
- The graph will show an initial increase in the number of atoms of B as A decays, reaching a peak, and then a decrease as B decays into C.
- This results in a curve that rises to a maximum and then falls, resembling a typical exponential growth followed by decay.
The suitable graph for the number of atoms of B vs. time is one that starts at zero, increases to a maximum, and then decreases over time.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
A sample of a radioactive nucleus A disintegrates to another radioactive nucleus B, which in turn disintegrates to some other stable nucleus C. Plot of a graph showing the variation of number of atoms of nucleus B vesus time is : (Assume that at t = 0, there are no B atoms in the sample)
View SolutionTwo Radioactive substances X and Y emit a and B particles respectively. Their disintegration constants are in the ratio 2 : 3. To have equal rate of disintegration of getting emission of a and particles, the ratio of number of atoms of X to that of Y at any time instant is
View Solution
Knowledge Check
There are two radio nuclei A and B.A is an α emitter and B a β emitter. Their disintegration constant are in the ratio of 1:2 What should be the ratio of number of atoms of A and B at any time t so that probabilities of getting alpha and beta particles are same at that instant?
A2:1B1:2CeDe_1There are two radio nuclei A and B is a α -emitter and B is β-emitter. Their disintegration constant are in the ratio of 1:2 . What should be the number of atoms ratio of A and B at time t=0 , so that initially probability of getting of α and β-particles are same.
A2:1B4:1C1:2D1:4Replace A,B,C by suitable numberals:
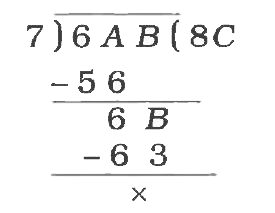 AA=1,B=3,C=9BA=2,B=3,C=9CA=1,B=6,C=9DA=1,B=6,C=8
AA=1,B=3,C=9BA=2,B=3,C=9CA=1,B=6,C=9DA=1,B=6,C=8
The mass number and the atomic number of uranium are 238 and 92 respectively. If on nuclear disintegration 6α−and4β-particles are emitted, find the mass number and atomic number of the atom formed.
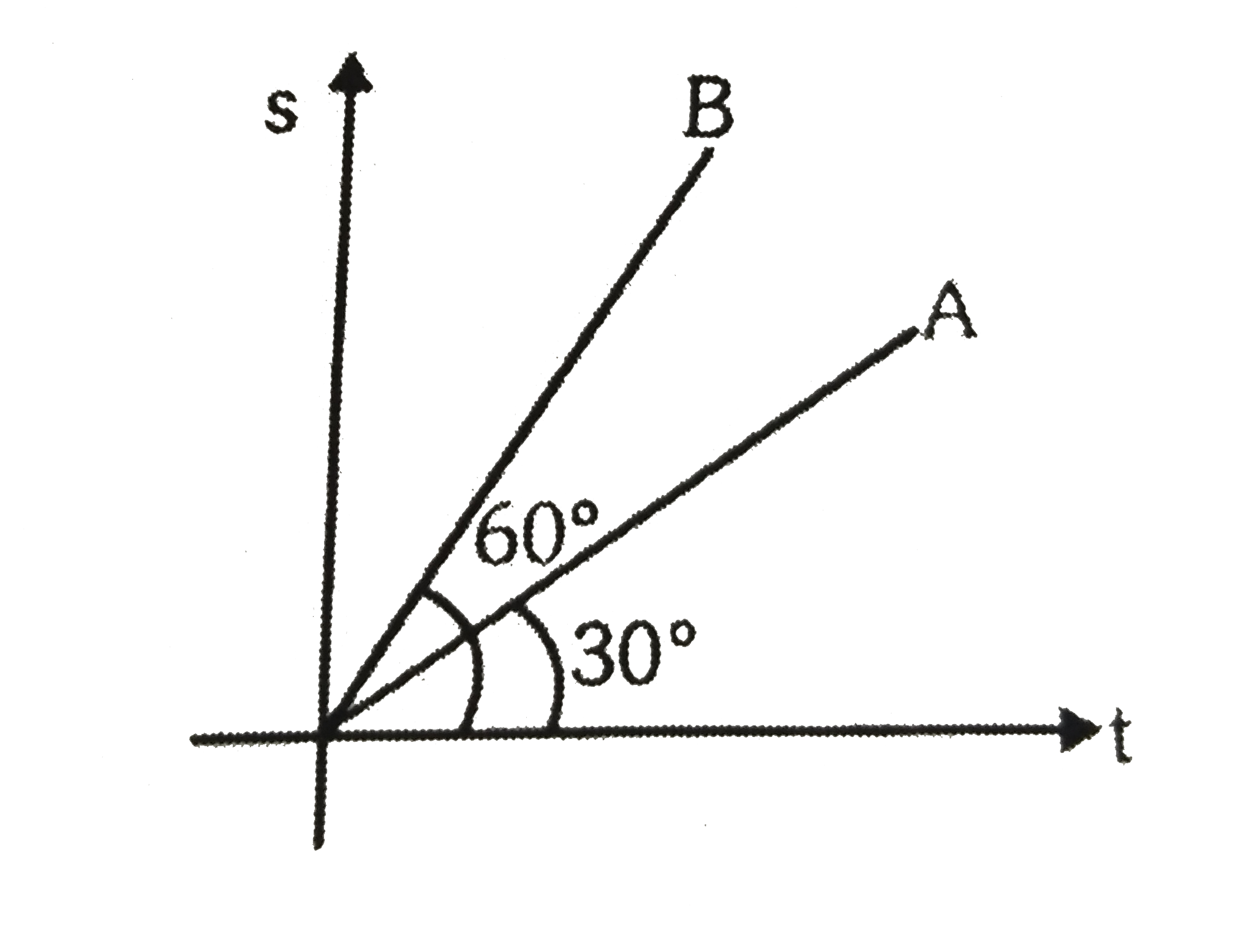
View Solutions-t graph of two particles A and B are shown in fig. Find the ratio of velocity of A to velocity of B.
View SolutionThe rate of disintegration of a radioactive substance is …………………………… to the number of atoms present at that time .
View SolutionReplace A,B and C by suitable numerals.
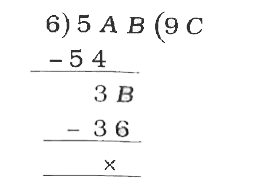
View SolutionA radioactive element A on disintegration gives two elements B and C. If B is helium and C is the element of atomic number 90 and atomic mass 234, the element A is:
View Solution
