A chord of length 6 cm is 4 cm away from the centre of circle. Find the diameter of the circle.
10 cm
6 cm
5 cm
8 cm
The correct Answer is:A
To find the diameter of the circle given that a chord of length 6 cm is 4 cm away from the center of the circle, we can follow these steps:
Step 1: Understand the Geometry
We have a circle with center O. There is a chord AB that is 6 cm long, and the perpendicular distance from the center O to the chord AB is 4 cm. Let C be the point where the perpendicular from O meets the chord AB.
Step 2: Bisect the Chord
Since the perpendicular from the center of the circle to the chord bisects the chord, we can say:
- AC = BC = half of AB
- Therefore, AC = BC = 6 cm / 2 = 3 cm.
Step 3: Set Up the Right Triangle
Now, we can form a right triangle OAC where:
- OC = 4 cm (the distance from the center to the chord),
- AC = 3 cm (half the length of the chord),
- OA = radius of the circle (which we need to find).
Step 4: Apply the Pythagorean Theorem
Using the Pythagorean theorem in triangle OAC:
OA2=OC2+AC2
Substituting the known values:
OA2=42+32
OA2=16+9
OA2=25
Taking the square root:
OA=√25=5 cm
Step 5: Find the Diameter
The diameter of the circle is twice the radius:
Diameter=2×OA=2×5=10 cm
Final Answer
The diameter of the circle is 10 cm.
---
We have a circle with center O. There is a chord AB that is 6 cm long, and the perpendicular distance from the center O to the chord AB is 4 cm. Let C be the point where the perpendicular from O meets the chord AB.
Since the perpendicular from the center of the circle to the chord bisects the chord, we can say:
- AC = BC = half of AB
- Therefore, AC = BC = 6 cm / 2 = 3 cm.
Now, we can form a right triangle OAC where:
- OC = 4 cm (the distance from the center to the chord),
- AC = 3 cm (half the length of the chord),
- OA = radius of the circle (which we need to find).
Using the Pythagorean theorem in triangle OAC:
OA2=OC2+AC2
Substituting the known values:
OA2=42+32
OA2=16+9
OA2=25
Taking the square root:
OA=√25=5 cm
The diameter of the circle is twice the radius:
Diameter=2×OA=2×5=10 cm
The diameter of the circle is 10 cm.
Similar Questions
Knowledge Check
A chord of length 30 cm is at a distance of 8 cm from the centre of a circle. The radius of the circle is :
A17 cmB23 cmC21 cmD19 cmLength of a tangent segment drawn from a point which is at a distnace 12.5 cm from the centre of a circle is 12cm , find the diameter of the circle.
A25 cmB24 cmC7 cmD14 cmA chord 6 cm long is at a distance of 4 cm from the centre of a circle. Find the length of a chord which is at a distance of 3 cm from the centre of the circle.
A10 cmB6 cmC8 cmD12 cm
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
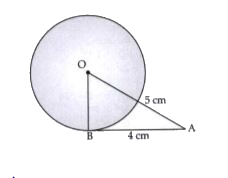
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
View SolutionThe length of a chord of a circle at a distance of 5 cm from the centre is 24 cm. The diameter of the circle is
View SolutionA 5 cm long perpendicular is drawn from the centre of a circle to a 24 cm long chord. Find the diameter of the circle.
View SolutionA chord of length 60 cm is at a distance of 16 cm from the centre of a circle . What is the radius (in cm ) of the circle ?
View Solution
