A square of the perimeter is q units, then its area is sq.units
(q^2)/16
(q^2)
(q^2)/4
(q^2)/64
The correct Answer is:A
To solve the problem, we need to find the area of a square when its perimeter is given as q units.
1. Understanding the Perimeter of a Square:
The perimeter P of a square is the sum of the lengths of all four sides. Since all sides of a square are equal, we can express the perimeter as:
P=4×side
2. Setting Up the Equation:
We are given that the perimeter P is equal to q units. Therefore, we can write:
4×side=q
3. Finding the Length of One Side:
To find the length of one side of the square, we rearrange the equation:
side=q4
4. Calculating the Area of the Square:
The area A of a square is given by the formula:
A=side2
Substituting the expression we found for the side:
A=(q4)2
5. Simplifying the Area:
Now we simplify the expression:
A=q216
6. Final Result:
Thus, the area of the square in square units is:
A=q216 square units
The perimeter P of a square is the sum of the lengths of all four sides. Since all sides of a square are equal, we can express the perimeter as:
P=4×side
We are given that the perimeter P is equal to q units. Therefore, we can write:
4×side=q
To find the length of one side of the square, we rearrange the equation:
side=q4
The area A of a square is given by the formula:
A=side2
Substituting the expression we found for the side:
A=(q4)2
Now we simplify the expression:
A=q216
Thus, the area of the square in square units is:
A=q216 square units
Similar Questions
Knowledge Check
A square of the perimeter is q units, then its area is sq.units
A(q^2)/16B(q^2)C(q^2)/4D(q^2)/64If the perimeter of a certain rectangle is 50 units and its area is 150 sq. units, then how many units is the length of its shorter side?/
यदि किसी आयत का परिमाप 50 इकाई है तथा इसका क्षेत्रफल 150 वर्ग इकाई है, तो इसकी छोटी भुजा की लंबाई कितनी इकाई है ?A12B15C10D9If the perimeter of a square is (4a+8)unit, then its area will be
A(a2+4a+4) sq unitB(10a2−a−8) sq unitC(a+2a2+4) sq unitD(4a2+4a−4) sq unit
The area of a sector whose perimeter is four times its radius r units, is (a) r24 sq. units (b) 2r2 sq. units (c) r2 sq. units (d) r22 sq. units
View SolutionThe area of a sector whose perimeter is four times its radius (r units) is
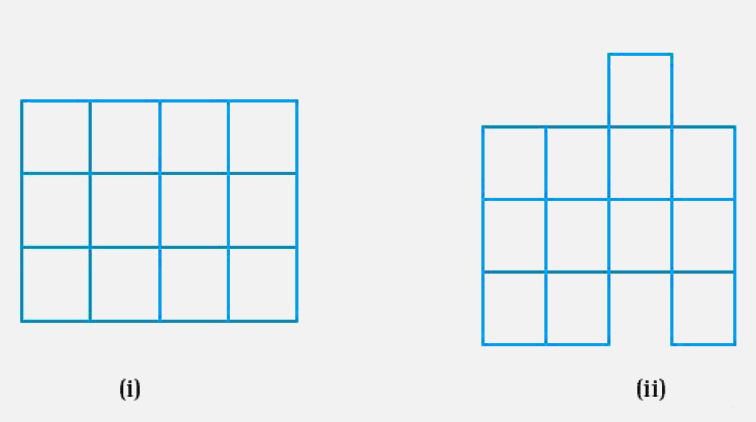
View SolutionIn Fig. 9.27
If (ii) is divided into squares of unit length, then its area is 13 unit squares.
View SolutionIf the perimeter of a square is (4a+8) unit,then its area will be
View SolutionThe area of a sector whose perimeter is four times its radius (r units) is
View Solution