If AD is the bisector of ∠BAC and AB = 10 cm, AC = 6 cm, BC = 12 cm, then find BD?
यदि AD, ∠BAC का समद्विभाजक है तथा AB = 10cm, AC = 6cm, BC = 12cm, तो BD ज्ञात करें।
6 cm
7.5 cm
8 cm
8.5 cm
The correct Answer is:B
To find the length of BD when AD is the bisector of angle BAC in triangle ABC, we can use the Angle Bisector Theorem. According to this theorem, the angle bisector divides the opposite side into segments that are proportional to the lengths of the other two sides.
1. Identify the given lengths:
- AB = 10 cm
- AC = 6 cm
- BC = 12 cm
2. Apply the Angle Bisector Theorem:
The Angle Bisector Theorem states that:
BDDC=ABAC
Let BD = x and DC = y. Since BC = BD + DC, we have:
x+y=12(1)
3. Set up the ratio using the theorem:
From the theorem:
xy=106=53
This implies:
3x=5y(2)
4. Substitute equation (1) into equation (2):
From equation (1), we can express y in terms of x:
y=12−x
Substitute this into equation (2):
3x=5(12−x)
Simplifying this gives:
3x=60−5x
3x+5x=60
8x=60
x=608=7.5
5. Find y using equation (1):
Substitute x back into equation (1):
y=12−7.5=4.5
6. Conclusion:
Therefore, BD = x = 7.5 cm.
Final Answer:
BD = 7.5 cm
- AB = 10 cm
- AC = 6 cm
- BC = 12 cm
The Angle Bisector Theorem states that:
BDDC=ABAC
Let BD = x and DC = y. Since BC = BD + DC, we have:
x+y=12(1)
From the theorem:
xy=106=53
This implies:
3x=5y(2)
From equation (1), we can express y in terms of x:
y=12−x
Substitute this into equation (2):
3x=5(12−x)
Simplifying this gives:
3x=60−5x
3x+5x=60
8x=60
x=608=7.5
Substitute x back into equation (1):
y=12−7.5=4.5
Therefore, BD = x = 7.5 cm.
BD = 7.5 cm
Similar Questions
Knowledge Check
- Question 1 - Select One
In figure AD is the bisector of ∠BAC. If BD=2cm,CD=3cmandAB=5cm. Find AC :
 A6 cmB7.5 cmC10 cmD15 cm
A6 cmB7.5 cmC10 cmD15 cm - Question 2 - Select One
In the given figure , if AD is the bisector of ∠BAC . If AB=10 cm , AC = 14 cm and BC = 6 cm , then find BD and DC .
 A2.5 cm , 3.5 cmB3 cm , 3 cmC3.5 cm , 4.5 cmD4 cm , 2 cm
A2.5 cm , 3.5 cmB3 cm , 3 cmC3.5 cm , 4.5 cmD4 cm , 2 cm - Question 3 - Select One
In the given figure , Ad is the bisector of ∠BAC. If AB = 10 cm , AC = 14 cm and BC = 8 cm , find BD and DC respectively .
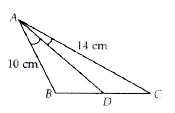 A4.7cm,3.3cmB3.3cm,4.7cmC4.3cm,3,5cmD3.5cm,4.3cm
A4.7cm,3.3cmB3.3cm,4.7cmC4.3cm,3,5cmD3.5cm,4.3cm
In the figure , AD is bisector of ˆA . If BC = 10 cm , BD = 6 cm , and AC = 6 cm, find AB.
View SolutionIf in △ABC, AD is the bisector of ∠AandD lies on BC. If AB = 6.4 cm, AC = 8 cm, BD = 5.6 cm, find DC.
View SolutionIn the given figure AD is the bisector of ∠A. If BD= 4 cm , DC = 3 cm and AB = 6cm . Find AC.
 View Solution
View SolutionIn ABC , the bisector of ∠A intersects BC in D . If AB=18cm , AC=15cm and BC=22cm , find BD
View SolutionIn Fig. 4.42, AD is the bisector of ∠BAC . If AB=10cm . AC=14cm and BC=6cm , find BD and DC . (FIGURE)
View Solution


