In an adiabatic process, volume of gas changes from 1200x10−6m3 to 300x10−6m3. Initial pressure of gas is 200 KPa. For the process is γ=1.5. Find work done by gas in the process.
-480J
-280J
480J
280J
To solve the problem of finding the work done by the gas during an adiabatic process, we will follow these steps:
Step 1: Identify the Given Values
- Initial volume, V1=1200×10−6m3
- Final volume, V2=300×10−6m3
- Initial pressure, P1=200kPa=200×103Pa
- γ=1.5
Step 2: Use the Adiabatic Condition
In an adiabatic process, the relationship between pressure and volume is given by:
PVγ=constant
Thus, we can write:
P1Vγ1=P2Vγ2
We need to find P2.
Step 3: Rearrange the Equation to Solve for P2
Rearranging the equation gives:
P2=P1(V1V2)γ
Step 4: Substitute the Known Values
Substituting the known values into the equation:
P2=200×103(1200×10−6300×10−6)1.5
Step 5: Calculate the Volume Ratio
Calculating the volume ratio:
V1V2=1200300=4
Step 6: Substitute the Volume Ratio Back
Now substitute the volume ratio back into the equation for P2:
P2=200×103×41.5
Step 7: Calculate 41.5
Calculating 41.5:
41.5=8
Step 8: Calculate P2
Now substitute this value back into the equation for P2:
P2=200×103×8=1600×103Pa=1600kPa
Step 9: Use the Work Done Formula
The work done by the gas in an adiabatic process is given by:
W=P1V1−P2V2γ−1
Step 10: Substitute the Values into the Work Done Formula
Substituting the values we have:
W=(200×103)(1200×10−6)−(1600×103)(300×10−6)1.5−1
Step 11: Calculate Each Term
Calculating each term:
- P1V1=200×103×1200×10−6=240J
- P2V2=1600×103×300×10−6=480J
Step 12: Substitute and Simplify
Now substitute these into the work done formula:
W=240−4800.5=−2400.5=−480J
Final Answer
The work done by the gas in this adiabatic process is:
W=−480J
- Initial volume, V1=1200×10−6m3
- Final volume, V2=300×10−6m3
- Initial pressure, P1=200kPa=200×103Pa
- γ=1.5
In an adiabatic process, the relationship between pressure and volume is given by:
PVγ=constant
Thus, we can write:
P1Vγ1=P2Vγ2
We need to find P2.
Rearranging the equation gives:
P2=P1(V1V2)γ
Substituting the known values into the equation:
P2=200×103(1200×10−6300×10−6)1.5
Calculating the volume ratio:
V1V2=1200300=4
Now substitute the volume ratio back into the equation for P2:
P2=200×103×41.5
Calculating 41.5:
41.5=8
Now substitute this value back into the equation for P2:
P2=200×103×8=1600×103Pa=1600kPa
The work done by the gas in an adiabatic process is given by:
W=P1V1−P2V2γ−1
Substituting the values we have:
W=(200×103)(1200×10−6)−(1600×103)(300×10−6)1.5−1
Calculating each term:
- P1V1=200×103×1200×10−6=240J
- P2V2=1600×103×300×10−6=480J
Now substitute these into the work done formula:
W=240−4800.5=−2400.5=−480J
The work done by the gas in this adiabatic process is:
W=−480J
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
a sample of gas with γ=1.5 is taken through an adiabatic process in which the volume is compressed from 1200 cm3 to 300 cm3 .If the initial pressure is 200 Pa. the absolute value of the workdone by the gas in the process = ___________ J.
View SolutionA sample of gas (γ=1.5) is taken through an adiabatic process in which the volume is compressed from 1600cm3→400cm3. If the initial pressure is 150kPa, (a) what is the final pressure and (b) how much work is done by the gas in the process?
View Solution
Knowledge Check
Find the work done by the gas in the process ABC.
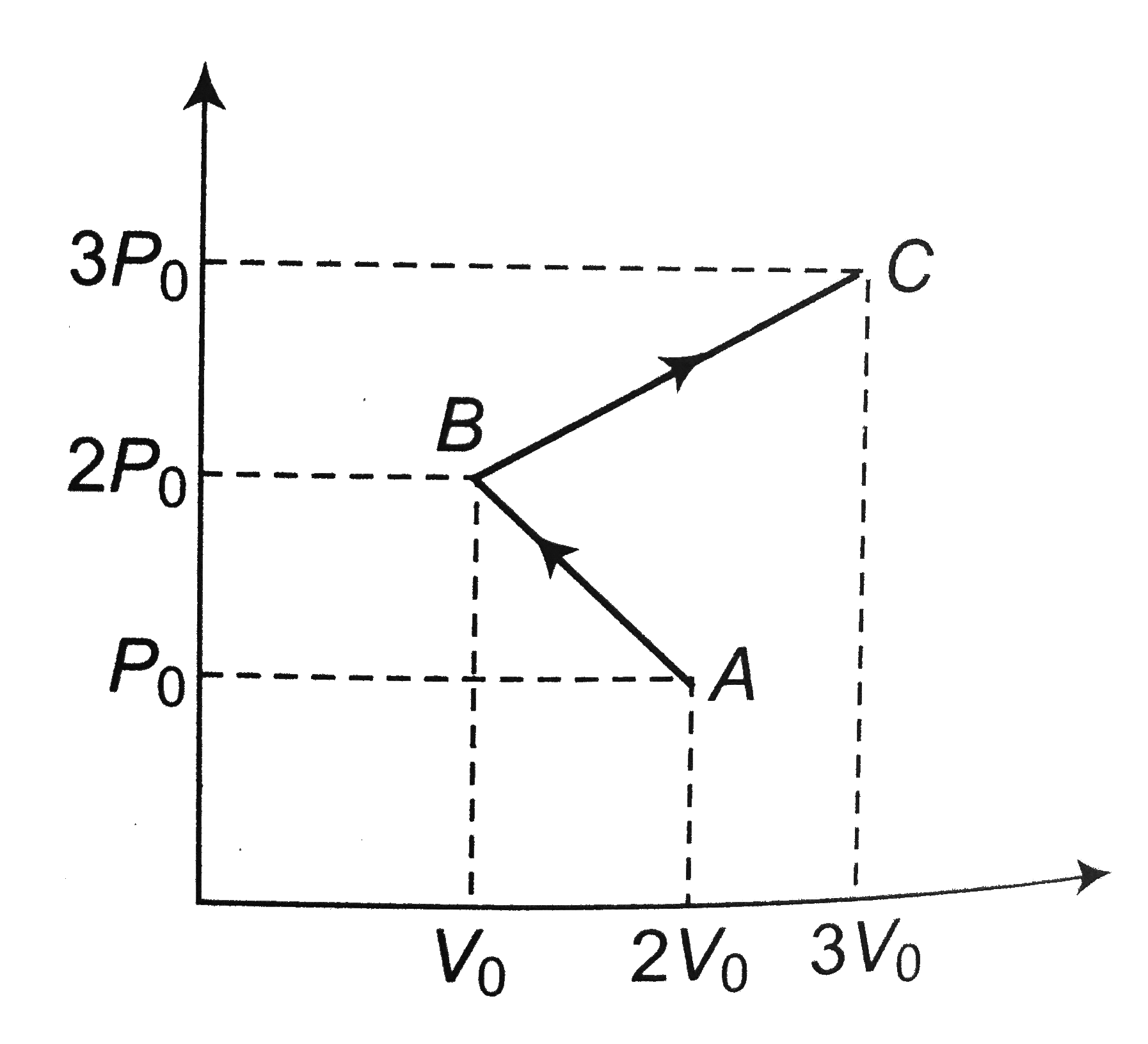 A32P0V0B52P0V0C72P0V0D4P0V0
A32P0V0B52P0V0C72P0V0D4P0V0Find work done by the gas in the process shown in figure.
 A52πatmLB52atmLC−32πatmLD−54πatmL
A52πatmLB52atmLC−32πatmLD−54πatmLFind work done by the gas in the process shown in figure :
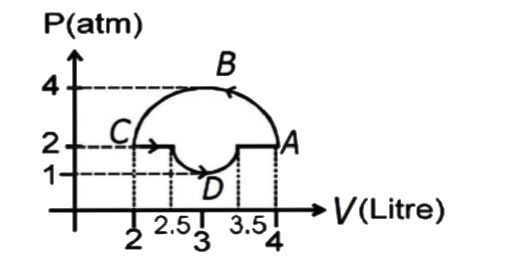 A52πatmLB52atmLC−32πatmLD−54πatmL
A52πatmLB52atmLC−32πatmLD−54πatmL
A sample of diatomic gas with y=1.5 is compressed from a volume of 1600 cc to 400 cc adiabatically. The initial pressure of gas was 1.5×105 Pa.Find the final pressure and work done by the gas in the process.
View SolutionDuring the expansion process the volume of the gas changes form 4m3 to 6m3 while the pressure change according to p=30V+100 where pressure is in Pa and volume is in m3. The work done by gas in N×102J. Find N.
View SolutionPressure and volume of a gas changes from (p0V0) to (p04,2V0) in a process pV2= constant. Find work done by the gas in the given process.
View SolutionThe pressure of a gas is 100 k Pa. if it is compressed from 1 m3 to 10dm3 , find the work done .
View SolutionAssertion: In a thermodynamic process, initial volume of gas is equal to final volume of gas. Work done by gas in this process should be zero
Reason: Work done by gas in isochoric process is zero.
View Solution
