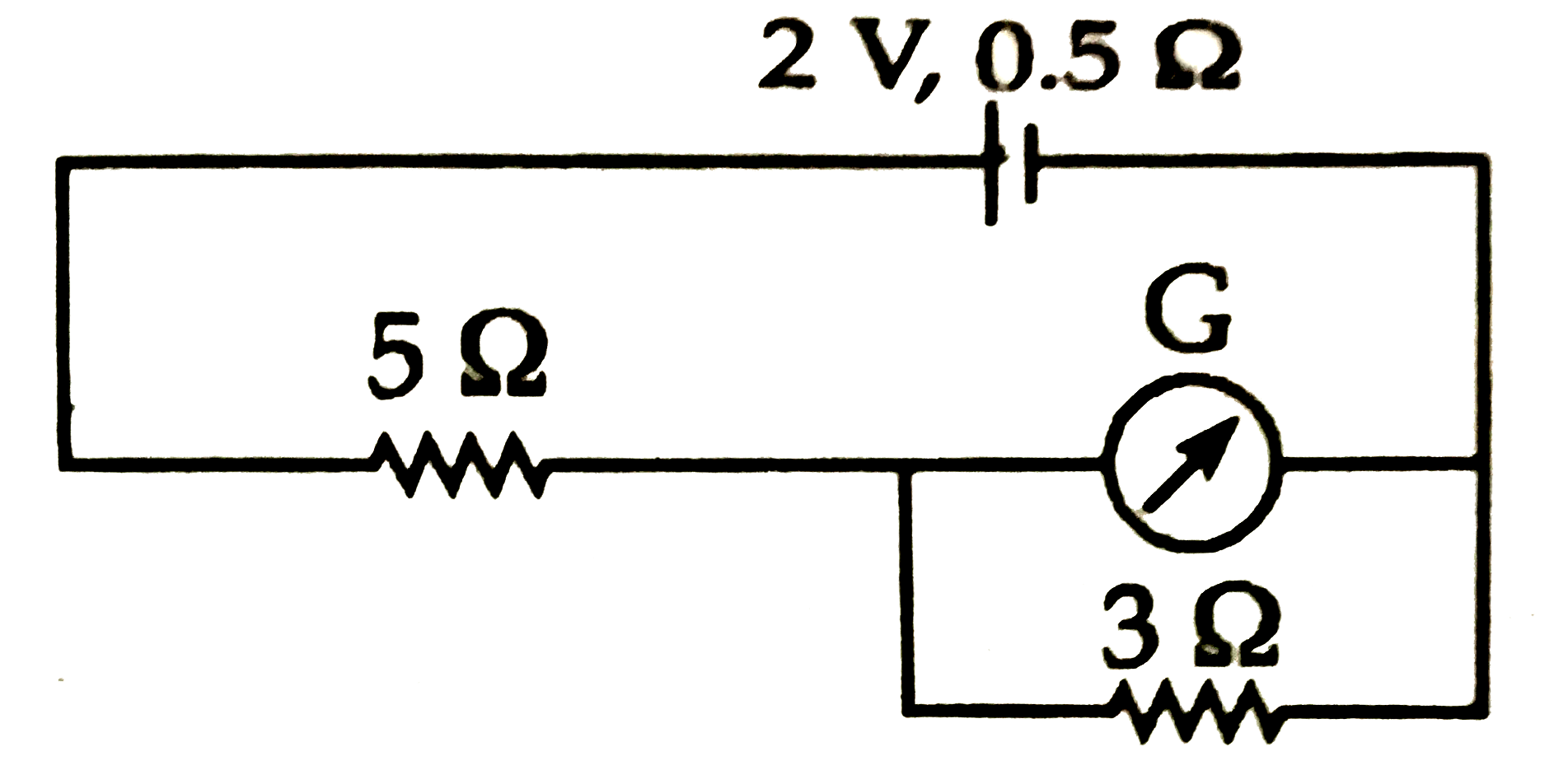A galvanometer of resistance 10kΩ can measure a maximum current 1 mA. A non-ideal battery of emf 6 V is connected across this galvanometer. A resistance 1Ω is also connected across the galvanometer. If the galvanometer reads a current 0.2 mA, the internal resistance of the battery is:
0.5Ω
1Ω
2Ω
4Ω
The correct Answer is:C
To solve the problem, we need to find the internal resistance of the battery given the parameters of the galvanometer and the current it reads.
1. Identify the Given Values:
- Resistance of the galvanometer, Rg=10kΩ=10,000Ω
- Maximum current the galvanometer can measure, Imax=1mA=0.001A
- Current reading of the galvanometer, Ig=0.2mA=0.0002A
- Resistance connected across the galvanometer, R=1Ω
- EMF of the battery, E=6V
2. Calculate the Total Resistance in the Circuit:
The total resistance Rtotal in the circuit is the sum of the galvanometer resistance and the additional resistance:
Rtotal=Rg+R=10,000Ω+1Ω=10,001Ω
3. Calculate the Potential Difference Across the Galvanometer:
The potential difference Vg across the galvanometer can be calculated using Ohm's law:
Vg=Ig×Rg=0.0002A×10,000Ω=2V
4. Determine the Total Voltage Drop in the Circuit:
The total voltage drop in the circuit is equal to the EMF of the battery minus the voltage drop across the internal resistance r of the battery:
E=Vg+Ig×r
Rearranging gives:
r=E−VgIg
5. Substitute the Known Values:
Substituting the known values into the equation:
r=6V−2V0.0002A=4V0.0002A=20,000Ω
6. Final Answer:
The internal resistance of the battery is:
r=20,000Ω
- Resistance of the galvanometer, Rg=10kΩ=10,000Ω
- Maximum current the galvanometer can measure, Imax=1mA=0.001A
- Current reading of the galvanometer, Ig=0.2mA=0.0002A
- Resistance connected across the galvanometer, R=1Ω
- EMF of the battery, E=6V
The total resistance Rtotal in the circuit is the sum of the galvanometer resistance and the additional resistance:
Rtotal=Rg+R=10,000Ω+1Ω=10,001Ω
The potential difference Vg across the galvanometer can be calculated using Ohm's law:
Vg=Ig×Rg=0.0002A×10,000Ω=2V
The total voltage drop in the circuit is equal to the EMF of the battery minus the voltage drop across the internal resistance r of the battery:
E=Vg+Ig×r
Rearranging gives:
r=E−VgIg
Substituting the known values into the equation:
r=6V−2V0.0002A=4V0.0002A=20,000Ω
The internal resistance of the battery is:
r=20,000Ω
Similar Questions
Knowledge Check
A galvanometer has a resistance of 3663Ω. A shunt S is connected across it such that (1/34) of the total current passes through the galvanometer. Then the value of the shunt (in Ω) is
A222ΩB111ΩC11ΩD22ΩA galvanometer has a resistance of 3663Ω. A shunt Sis connected across it such that (1/34) of the total current passes through the galvanometer. Then the value of the shunt is :
A222ΩB111ΩC11ΩD22ΩThe deflection of galvanometer falls from 60 to 30, when 12 Ω shunt is connected across it. The galvanometer resistance is
A12ΩB36ΩC24ΩD30Ω
A galvanometer of resistance 40Ω can measure a current of 10mA To convert it into a voltmeter of range 8V the required resistance is ___________ Ω.
View SolutionA galvanometer of 25Ω resistance can read a maximum current of 6 mA . It can be used as a voltmeter to measure a maximum of 6 V by connecting a resistance to the galvanometer. Identify the correct choice in the given answers
View SolutionCalculate the value of the shunt resistance when connected across a galvanometer of resistance 18Ω will allow 1/10 th of the current to pass through the galvanometer.
View SolutionA galvanometer of resistance 50 Ω gives a full scale deflection for a current 5×10−4 A. The resistance that should be connected in series with the galvanometer to read 3 V is
View SolutionIf the galvanometer current is 10 mA, resistance of the galvanometer is 40Ω and shunt of 2Ω is connected to the galvanometer, the maximum current which can be measured by this ammeter is
View Solution