A capacitor is connected to a 20V battery and 10 ohm resistance. The potential difference across the capacitor rises from 0V to 2V in 10μs. Find capacitance of capacitor (given ln(109)=0.105)
9.5μF
12μF
14.5μF
15μF
To find the capacitance of the capacitor, we can use the formula for the voltage across a charging capacitor in an RC circuit:
V(t)=V0(1−e−t/(RC))
Where:
- V(t) is the voltage across the capacitor at time t
- V0 is the maximum voltage (20V in this case)
- R is the resistance (10 ohms)
- C is the capacitance (which we need to find)
- t is the time (10 microseconds or 10×10−6 seconds)
Step 1: Set up the equation
Given that the voltage across the capacitor rises from 0V to 2V in 10 microseconds, we can substitute the known values into the equation:
2=20(1−e−10×10−6/(10C))
Step 2: Simplify the equation
Divide both sides by 20:
220=1−e−10×10−6/(10C)
This simplifies to:
110=1−e−10×10−6/(10C)
Step 3: Isolate the exponential term
Rearranging gives:
e−10×10−6/(10C)=1−110
This simplifies to:
e−10×10−6/(10C)=910
Step 4: Take the natural logarithm
Taking the natural logarithm of both sides:
−10×10−610C=ln(910)
Step 5: Solve for C
This can be rewritten as:
−10−5C=ln(910)
Now, we can isolate C:
C=−10−5ln(910)
Step 6: Substitute the value of ln(10/9)
Given that ln(10/9)=0.105, we can use this value:
C=−10−5−0.105=10−50.105
Step 7: Calculate C
Calculating this gives:
C≈9.52×10−6 F=9.52μF
Final Answer
Thus, the capacitance of the capacitor is approximately:
C≈9.5μF
- V(t) is the voltage across the capacitor at time t
- V0 is the maximum voltage (20V in this case)
- R is the resistance (10 ohms)
- C is the capacitance (which we need to find)
- t is the time (10 microseconds or 10×10−6 seconds)
Given that the voltage across the capacitor rises from 0V to 2V in 10 microseconds, we can substitute the known values into the equation:
Divide both sides by 20:
Rearranging gives:
Taking the natural logarithm of both sides:
This can be rewritten as:
Given that ln(10/9)=0.105, we can use this value:
Calculating this gives:
Thus, the capacitance of the capacitor is approximately:
Similar Questions
A capacitor is connected to a 20 V battery through a resistance of 10Ω. If is found that the potential difference across the capacitor rises to 2V in1μs. The capacitance of the capacitor is ___________μF.
View SolutionA capacitor is connected to a 20 V battery through a resistance of 10Ω. If is found that the potential difference across the capacitor rises to 2V in1μs. The capacitance of the capacitor is ___________μF.
View Solution
Knowledge Check
- Question 1 - Select One
given that potential differene across 1μF capacitor is 10V. Then,
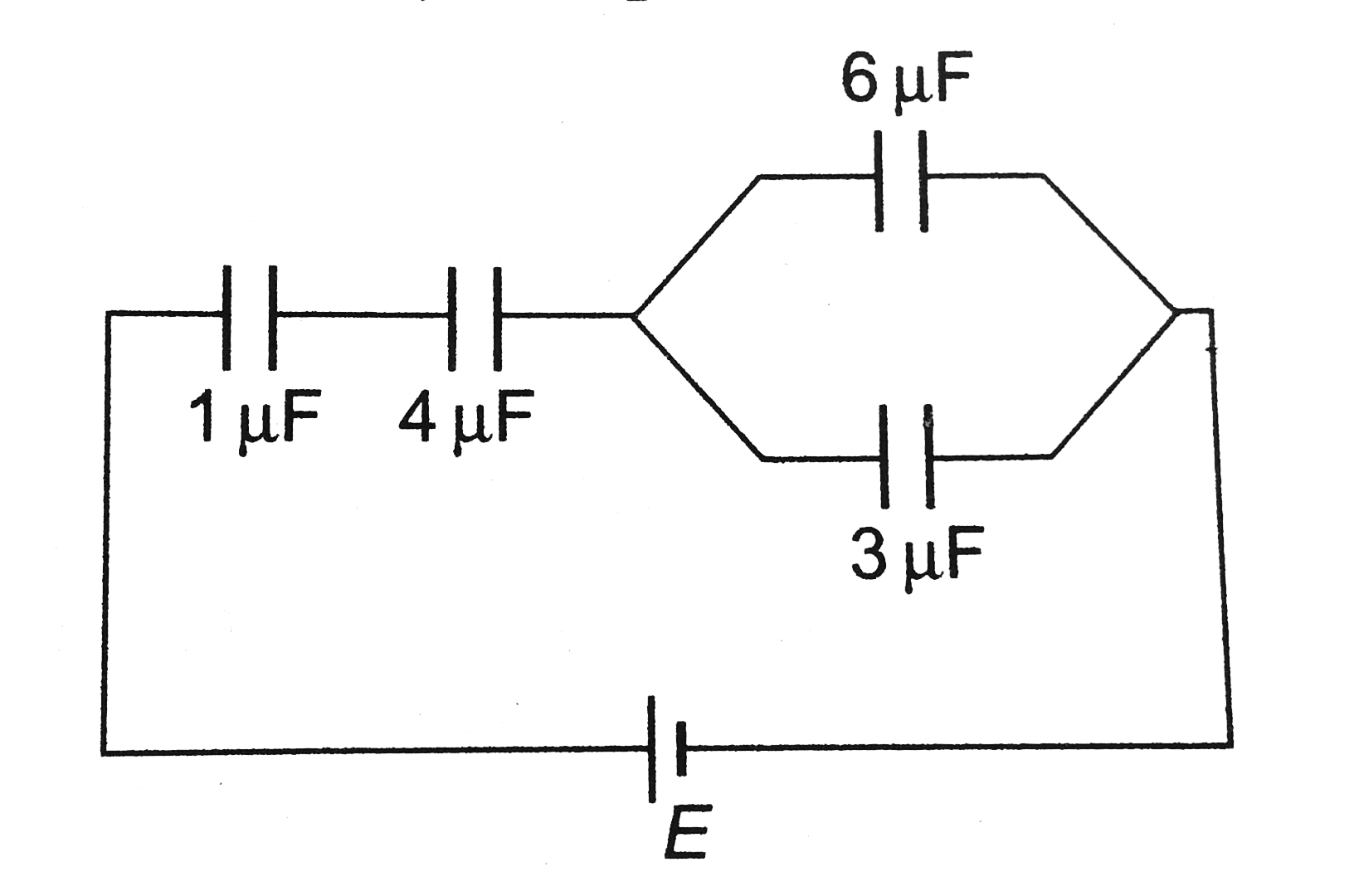 Apotential difference across 4μF capacitor is 40VBpotential difference acros 4μF capacitor is 2.5VCpotential diference across 3μFe capacitor is 5VDvalue of E is 50V
Apotential difference across 4μF capacitor is 40VBpotential difference acros 4μF capacitor is 2.5VCpotential diference across 3μFe capacitor is 5VDvalue of E is 50V - Question 2 - Select One
If the potential difference across a capacitor is increased from 10V to 30V, then the energy stored with the capacitor.
Aincreases to 3 times its initial value.Bincreases to 9 times its initial value.Cincreases to 27 times its initial value.Ddecreases to 1/3 times its initial value. - Question 3 - Select One
The 500μF capacitor is charged at a steady rate of 100μC/s. The potential difference across the capacitor will be 10 V after an interval of
A80secB50secC20secD40sec
A capacitor is connected to a 36 V battery through a resistance of 10Ω. It is found that the potential difference across the capacitor rises to 4.0 V in 1μs. Find the capacitance of the capacitor. (Given :ln3=1.0986,ln2=0.693)
View SolutionA capacitor is connected to a 12 V battery through a resistance of (10Ω).It is found that the potential difference across the capacitor rises to 4.0 V in 1(mu)s. find the capacitance of the capacitor.
View SolutionA capacitor is connected to a 36 V battery through a resistance of 20Ω. It is found that the potential difference across the capacitor rises to 12.0 V in 2μs. Find the capacitance of the capacitor.
View SolutionA capacitor of capacitance C is connected to a 6.0V battery through a resistance of 5Ω .The potential difference between the plates rises from zero to 3.0V in 6.9μS.The value of C
View SolutionThe 500μF capacitor is charged at a steady rate of 100μC/s. The potential difference across the capacitor will be 10 V after an interval of
View Solution

