Comprehension:
The following questions are based on the information given below:
In a school of 4000 students 3000 know English, 2000 know French and 500 know Hindi, 1500 know French and English, 300 know French and Hindi, 200 know English and Hindi and 50 know all the three languages.
How many know at least one language?
A. 3500
B. 3000
C. 1850
D. 3550
A
B
C
D
The correct Answer is:A
To find out how many students know at least one language, we can use the principle of inclusion-exclusion. Let's break down the problem step by step.
Step 1: Define the variables
Let:
- E = number of students who know English = 3000
- F = number of students who know French = 2000
- H = number of students who know Hindi = 500
- EF = number of students who know both English and French = 1500
- FH = number of students who know both French and Hindi = 300
- EH = number of students who know both English and Hindi = 200
- EFH = number of students who know all three languages = 50
Step 2: Apply the inclusion-exclusion principle
The formula for the number of students who know at least one language is given by:
|E∪F∪H|=|E|+|F|+|H|−|EF|−|FH|−|EH|+|EFH|
Step 3: Substitute the values into the formula
Substituting the values we have:
|E∪F∪H|=3000+2000+500−1500−300−200+50
Step 4: Calculate the total
Now, let's perform the calculations step by step:
1. Add the number of students who know each language:
3000+2000+500=5500
2. Subtract the students who know two languages:
5500−1500−300−200=4500
3. Add back the students who know all three languages:
4500+50=4550
Step 5: Final calculation
The total number of students who know at least one language is:
|E∪F∪H|=4550
Conclusion
The number of students who know at least one language is 3550. Therefore, the correct answer is D. 3550.
Let:
- E = number of students who know English = 3000
- F = number of students who know French = 2000
- H = number of students who know Hindi = 500
- EF = number of students who know both English and French = 1500
- FH = number of students who know both French and Hindi = 300
- EH = number of students who know both English and Hindi = 200
- EFH = number of students who know all three languages = 50
The formula for the number of students who know at least one language is given by:
Substituting the values we have:
Now, let's perform the calculations step by step:
3000+2000+500=5500
5500−1500−300−200=4500
4500+50=4550
The total number of students who know at least one language is:
|E∪F∪H|=4550
The number of students who know at least one language is 3550. Therefore, the correct answer is D. 3550.
Similar Questions
Knowledge Check
Comprehension:
The following questions are based on the information given below:
In a school of 4000 students 3000 know English, 2000 know French and 500 know Hindi, 1500 know French and English, 300 know French and Hindi, 200 know English and Hindi and 50 know all the three languages.
How many know only two languages?A450B500C1850D1580Comprehension:
The following questions are based on the information given below:
In a school of 4000 students 3000 know English, 2000 know French and 500 know Hindi, 1500 know French and English, 300 know French and Hindi, 200 know English and Hindi and 50 know all the three languages.
How many do not know any of the three languages?AA.500BB.450CC.550DD.600The structure given below is know as
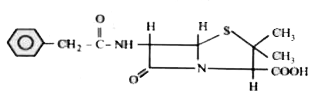 APenicillin FBPenicillin GCPenicillin KDAmpicillin
APenicillin FBPenicillin GCPenicillin KDAmpicillin
In a committee, 50 people speak Hindi, 20 speak English and 10 speak both Hindi and English . How many speak at least one of these two languages ?
View SolutionOne who knows many languages.
View SolutionHow many students learn English one French?
View SolutionWhich of the following is know as anhydron ?
View SolutionWhich of the following species is/are not know?
View Solution
