ΔABC~ΔPQR. If AM and PN are altitudes of ΔABCandΔPQR respectively and AB2:
PQ2=4:9 then AM:PN=
16:81
4:9
3:2
2:3
To solve the problem, we need to find the ratio of the altitudes AM and PN of triangles ΔABC and ΔPQR respectively, given that the squares of the sides AB2 and PQ2 are in the ratio 4:9.
1. Understanding the Given Ratio:
We are given that:
AB2PQ2=49
This implies that the ratio of the sides AB and PQ can be found by taking the square root of the ratio of their squares.
2. Finding the Ratio of the Sides:
Taking the square root of both sides:
ABPQ=√49=23
3. Using the Property of Similar Triangles:
Since ΔABC∼ΔPQR, the ratios of corresponding sides are equal. Therefore, we have:
ABPQ=AMPN
This means:
AMPN=23
4. Expressing the Ratio of Altitudes:
From the above, we can conclude that:
AM:PN=2:3
Final Answer:
Thus, the ratio of the altitudes AM and PN is:
AM:PN=2:3
We are given that:
AB2PQ2=49
This implies that the ratio of the sides AB and PQ can be found by taking the square root of the ratio of their squares.
Taking the square root of both sides:
ABPQ=√49=23
Since ΔABC∼ΔPQR, the ratios of corresponding sides are equal. Therefore, we have:
ABPQ=AMPN
This means:
AMPN=23
From the above, we can conclude that:
AM:PN=2:3
Thus, the ratio of the altitudes AM and PN is:
AM:PN=2:3
Similar Questions
Knowledge Check
What is value of x + y, if ΔABC and ΔPQR are similar?
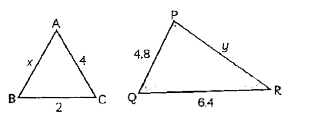 A12.8 cmB14.3 cmC12.5 cmD14 cm
A12.8 cmB14.3 cmC12.5 cmD14 cmΔABCandΔPQR are congruent if _______
AAB=BC=AC and PQ=QR=PRB∠A=∠P,∠B=∠Qand∠C=∠RCAB=PQ,BC=QRand∠B=∠QDAB=PR,BC=RTand∠C=∠TArea of ΔABC=30cm2. D and E are the mid - points of BC and AB respectively. Find A(ΔBDE) :
A10B7.5C15Dnone of these
ΔABC~ΔPQR. If AB=4cm, PQ=6cm and QR=9cm. Find BC.
View SolutionΔABC~ΔPQR and ar(ΔABC)=4ar(ΔPQR) IF BC=12cm then find QR
View SolutionΔABC~ΔPQR. If A(ΔABC)=25, A(ΔPQR)=16 find AB:PQ.
View SolutionPerimeter of two similar triangles ΔABC and ΔPQR are 36 cm and 24 cm respectively and if PQ = 10. Find AB.
View SolutionIf in ΔABC, seg AM is the median, AB2+AC2=410 and BC=12 then AM=?
View Solution
