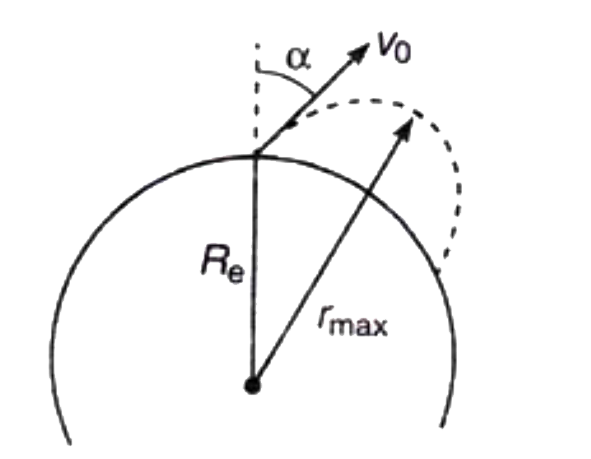
m द्रव्यमान का एक प्रक्षेप्य ऊर्ध्वाधर से $a l p h = 60^{\circ}$ कोण पर पृथ्वी की सतह से दागा जाता है। $υ_{0}$ प्रारंभिक चाल, $\sqrt{\frac{G M_{e}}{R_{e}}}$ के बराबर है। अधिकतम ऊंचाई, जहाँ तक प्रक्षेप्य पृथ्वी की सतह से उठ सकता है,
$\frac{R_{e}}{x}$ है। x का मान ज्ञात कीजिए।
G = सार्वत्रिक गुरुत्वाकर्षण स्थिरांक
$M_{e}$ = पृथ्वी का द्रव्यमान
$R_{e}$ = पृथ्वी की त्रिज्या

A

2

B

4

C

6

D

8

Text Solution

Verified by Experts

The correct Answer is:A

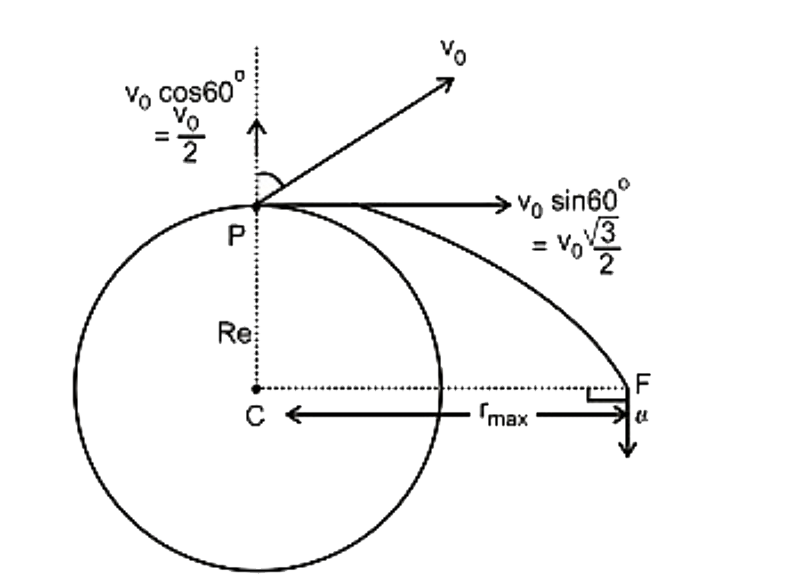
P और F स्थिति पर C के परितः कोणीय संवेग के संरक्षण द्वारा,
$m v_{0} \frac{\sqrt{3}}{2} R_{e} = m v r_{max}$
$\Rightarrow v = \frac{\sqrt{3} R_{e} v_{0}}{2 r_{max}}$ .... (i)
P और F के बीच यांत्रिक ऊर्जा के संरक्षण द्वारा,
$\frac{1}{2} m v_{0}^{2} - \frac{G M_{e} m}{R_{e}} = \frac{1}{2} m v^{2} - \frac{G M_{e} m}{r_{max}}$ ....(ii)
(i) को (ii) में रखने पर, $\frac{1}{2} m v_{0}^{2} - \frac{G M_{e} m}{R_{e}} \frac{1}{2} m \frac{3 R^{2} v_{0}^{2}}{4 r_{max}^{2}} - \frac{G M_{e} m}{r_{max}}$
$v_{0} = \sqrt{\frac{G M_{e}}{R}} \Rightarrow \frac{1}{2} m \frac{G M_{e}}{R_{e}} - \frac{G M_{e} m}{R_{e}} = \frac{3}{8} \frac{m R_{e}^{2}}{r_{max}^{2}} \frac{G M_{e}}{R} - \frac{G M_{e} m}{r_{max}}$
$\Rightarrow \frac{1}{2 R_{e}} - \frac{1}{R_{e}} = \frac{3 R}{8 r_{max}^{2}} - \frac{1}{r_{max}}$
$\Rightarrow \frac{1}{2 R_{e}} = \frac{3 R_{e} - 8 r_{max}}{8 r_{max}^{2}} \Rightarrow 4 r_{max}^{2} - 8 R_{e} r_{max} + 3 R_{e}^{2} = 0$
$r_{max}$ में द्विघात को हल करने पर, हमें प्राप्त होता है,
$r_{max} = \frac{8 R_{e} \pm \sqrt{16} R_{e}}{8} = \frac{8 R_{e} \pm 4 R_{e}}{8}$
$\Rightarrow r_{max} = \frac{8 R_{e} + 4 R_{e}}{8} = \frac{12 R_{e}}{8} = \frac{3 R_{e}}{2}$
$∴ h_{max} = r_{max} - R_{e} = \frac{3 R_{e}}{2} - R_{e} = \frac{R_{e}}{2}$
$∴ x = 2$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

NTA MOCK TESTS-NEET TEST 41-भौतिक विज्ञान

Home
Ask Doubt
Profile