L लंबाई और M द्रव्यमान का एक एकसमान बेलन, जिसके अनुप्रस्थ काट का क्षेत्रफल A है, को स्प्रिंग नियतांक K के एक द्रव्यमान रहित स्प्रिंग द्वारा एक निश्चित बिंदु से, इसे ऊर्ध्वाधर लंबाई के सापेक्ष इस प्रकार निलंबित किया गया है कि साम्यावस्था में इसका आधा भाग σ घनत्व के द्रव में डूब जाता है। साम्यावस्था में स्प्रिंग का विस्तार x0 है

Mg/K
(Mg/K)(1−LAα/M)
(Mg/K)[1−(LAσ/2M)]
MgLA/Kσ
The correct Answer is:C
मान लीजिए कि x0= साम्यावस्था की स्थिति में विस्तार
F=स्प्रिंग में प्रत्यानयन बल
F=Kx0
बेलन पर नीचे की ओर कार्यरत कुल बल
= Mg - ऊपर की ओर प्रणोद
=Mg−(L/2)×A×σ×g
साम्यावस्था के लिए Kx0=Mg−(LAσg/2)
Kx0=Mg[1−(LAσ/2M)]
x0=Mg/K[1−(LAσ/2M)]
Topper's Solved these Questions
Similar Questions
पूर्ण सूर्य ग्रहण के समय, सौर विकिरण के स्पेक्ट्रम में:
View Solutionहाइड्रोजन परमाणु का आयनीकरण विभव 13.6 eV है। तलस्थ अवस्था में हाइड्रोजन परमाणुओं को फोटॉन ऊर्जा 12.1 eV की एकवर्णी विकिरण से उत्तेजित होते हैं। बोहर के सिद्धांत के अनुसार हाइड्रोजन परमाणुओं द्वारा उत्सर्जित स्पेक्ट्रमी रेखाएँ होंगी:
View SolutionIn a U-tube, the radii of the two pillars are respectively r_1 " और " r_2 Huh. When rho (theta = 0^@) घनत्व का एक द्रव इसमें भरा जाता है, तो दो भुजाओं के स्तर में h | का अंतर देखा जाता है। द्रव का पृष्ठ तनाव है:
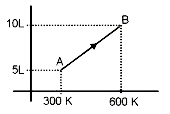
View Solutionचित्र में दर्शाये अनुसार एक आदर्श गैस के एक मोल को A→B अनुसार लिया गया है। प्रक्रम में निहित कार्य का परिमाण है: (R=253JmolK)
View Solutionविरंजक चूर्ण में इसके एक घटक के रूप में एक ऑक्सोअम्ल का लवण होता है। इस अम्ल का एनहाइड्राइड है:
View Solutionएक द्रव, जल में अमिश्रणीय है जो कि 0.983 atm के दाब और 95.2^(@)C पर भाप आसवित है। आसुत में जल के प्रति ग्राम में उपस्थित द्रव का द्रव्यमान क्या है। द्रव का मोलर द्रव्यमान 134.3 g/mol है और जल का वाष्प दाब 0.84 atm है। साथ ही, शुद्ध द्रव का वाष्प दाब 0.143 atm है।
View Solutionजब AgNO_(3) के विलयन को आधिक्य में CoCl_(3).XNH_(3) विलयन के 1M में मिलाया जाता है, तो AgCI के एक मोल का निर्माण होता है? 'X' का मान क्या है? (माना लीजिए कि उपसहसंयोजन संख्या 6 है।)
View Solutionऐडिनिन न्यूक्लिक अम्ल के न्यूक्लियोटाइडों के निर्माण में शामिल दो प्यूरीन क्षारों में से एक है। ऐडिनिन का अणुसूत्र CxHxNx होता है, तो 'x' का मान है
View Solutionएक आदर्श गैस के दस मोलों को एक बंद पात्र में भरा जाता है । पात्र में बेलन और पिस्टन के प्रकार की व्यवस्था है और 0.821 atm पर गैस का दाब स्थिर रहता है। निम्नलिखित में से कौन सा आलेख logV और logT के परिवर्तन का सही निरूपण करता है? (V= आयतन(लीटर में) और T= ताप (केलिवन में)
View Solution27^@ C और 760 टॉर पर N_2O_4 के 20 % अणुओं को गैस के एक नमूने में वियोजित किया जाता है | साम्य पर मिश्रण का घनत्व क्या होगा ?
View Solutionगोल्ड में 407 pm कोर लंबाई के साथ एक fcc जालक होता है। गोल्ड परमाणु का व्यास है
View Solutionसल्फर के एक यौगिक में द्रव्यमान द्वारा 8% सल्फर उपस्थित होता है। यौगिक के न्यूनतम आण्विक द्रव्यमान की गणना कीजिए।
View Solutionनिम्नलिखित में से किस औषधि का उपयोग एक पीड़ाहारी के रूप में किया जाता है?
View Solutionएक लीटर के पात्र में, एथेनॉल और एसीटिक अम्ल के बीच अभिक्रिया होने से एथिल ऐसीटेट का निर्माण होता है और साम्यावस्था को निम्न रूप में दर्शाया जाता है, CH_3COOH (l) + C_2H_5OH (l) to CH_3COOC_2H_5 (l) +H_2O(l) 293 K पर, यदि एक एसीटिक अम्ल के 1.00 मोल और एथेनॉल के 0.18 मोल से अभिक्रिया प्रारंभ होती है, तो अंतिम साम्यावस्था मिश्रण में एथिल एसीटेट का 0.171 मोल प्राप्त होता है। साम्य स्थिरांक की गणना कीजिए।
View Solutionएक बंद ऊष्मारोधी पात्र में एक द्रव को इसके तापमान को बढ़ाने के लिए एक छड़ की सहायता से विडोलित किया जाता है। इस प्रक्रम में निम्नलिखित में से कौन सा सही है?
View Solutionकैल्शियम क्लोराइड का उपयोग एक निर्जलीकारक के रूप में किया जाता है क्योंकि
View Solution
