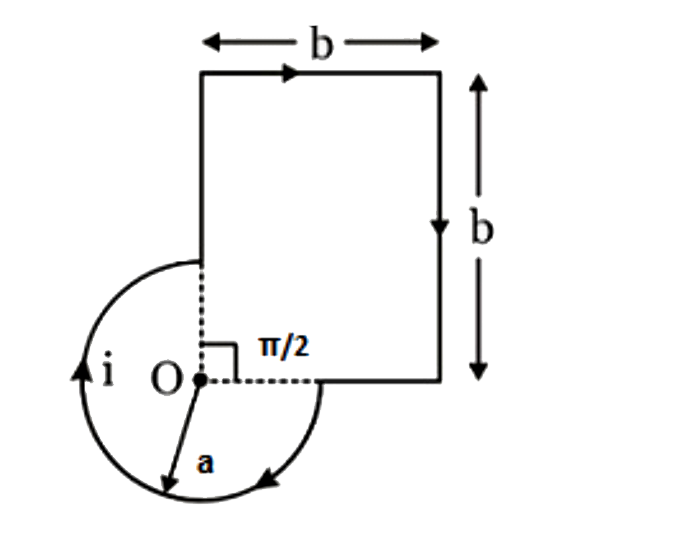
जैसा कि दर्शाया गया है, धारावाही कुंडली के कारण O (वृत्ताकार भाग का केंद्र) पर चुंबकीय क्षेत्र का परिमाण है:

A

$\frac{μ_{0} i}{4 π} (\frac{4 π}{a} + \frac{\sqrt{2}}{b})$

B

$\frac{μ_{0} i}{2 π} (\frac{3 π}{2 a} + \frac{\sqrt{2}}{b})$

C

$\frac{μ_{0} i}{2 π} (\frac{π}{3 a} + \frac{3}{\sqrt{2 b}})$

D

$\frac{μ_{0} i}{4 π} (\frac{3 π}{a} + \frac{\sqrt{2}}{b})$

Text Solution

Verified by Experts

The correct Answer is:D

वृत्ताकार खंड के कारण चुंबकीय क्षेत्र = $\frac{3}{4} . \frac{μ_{0} i}{2 a}$
एक सीधे तार खंड के कारण
$= \frac{μ_{0} i}{4 π b} ({sin 45}^{\circ} + {sin 0}^{\circ}) = \frac{μ_{0} i}{4 \sqrt{2} π b}$
नेट क्षेत्र
$= \frac{3 μ_{0} i}{8 a} + 2 \times \frac{μ_{0} i}{4 \sqrt{2} π b} = \frac{μ_{0} i}{4 π} (\frac{3 π}{a} + \frac{\sqrt{2}}{b})$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

NTA MOCK TESTS-NEET TEST NO 98-भौतिक विज्ञान

Home
Ask Doubt
Profile