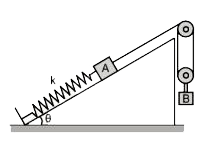
घर्षण हर जगह अनुपस्थित है और धागे, स्प्रिंग और घिरनियाँ द्रव्यमान रहित हैं। यदि mA=mB = m है, तब छोटे दोलनों के लिए निकाय की कोणीय आवृत्ति कितनी होगी?
√2k4m
√4k5m
√6k7m
√8k5m
The correct Answer is:D
माना कि X0 साम्यावस्था में स्प्रिंग में विस्तार है। A और B की साम्यावस्था निम्न देती है,
T=kx0+mgsinθ
...(i)
तथा 2T = mg
...(ii)
यहाँ, T डोरी में तनाव है। अब, मान लीजिए कि A आगे अपनी माध्य स्थिति से x दूरी से विस्थापित पुनः हो गया है और इस समय इसकी चाल v है। तब B,x2 से कम हो जाता है और इस क्षण B की चाल होगी।
इस स्थिति में निकाय की कुल ऊर्जा होगी:
E=12k(x+x0)2+12mAv2
+12mB(v2)2+mAghA_mBghB
या E=12k(x+x0)2+12mv2
+18mv2+mgxsinθ−mgx2
या E=12k(x+x0)2+58mv2
+mgxsinθ=mgx2
चूँकि, E नियतांक है,
dEdt=0
या 0=k(x+x0)dxdt+54mv(dvdt)
+mg(sinθ)(dxdt)−mg2(dxdt)
dxdt=v रखने पर,
dvdt=a
तथा kx2+mgsinθ=mg2
[समीकरण (i) और (i) से]
हमें प्राप्त होता है, 54ma=
-kx
चूँकि a∝−x
गति सरल आवर्त है, जिसका आवर्त काल है:
T=tπ√∣∣xa∣∣=2π√5m4k
ω=2πT=√4k5m
Topper's Solved these Questions
Similar Questions
यदि 2713Al नाभिक की त्रिज्या 3.6 फर्मी अनुमानित की जाती है तब 12552Te नाभिक की त्रिज्या लगभग है:
View Solutionनीचे दिखाए गए परिपथ में, i1 और i2 क्रमश: L1 और L2 से प्रवाहित धारा के स्थायी-अवस्था मान हैं, तब i1 है

View Solutionयदि A और B सममित आव्यूह हैं तो :
BA−2AB........... है ।
View Solutionयदि A=[axya] और यदि xy=1, तब det(AAT) के बराबर है
View Solutionस्प्रिंग द्रव्यमान निकाय
View Solutionयदि किसी भिन्न का अंश, हर से 2 कम है और यदि हर में 1 जोडा जाए तो यह 12 हो जाता है तब वह भिन्न होगी ?
View SolutionNH_3 के विरचन की मानक एन्थैल्पी - 46.0 kJ/mol है। यदि H_2 और N_2 की बंध एन्थैल्पी क्रमशः - 436 kJ/mol और - 712 kJ/mol है, तब NH_3 में N - H बंध की औसत बंध एन्थैल्पी क्या होगी?
View Solutionप्रथम कोटि अभिक्रिया के लिए निम्नलिखित में से कौन सा सही है/हैं? (a अभिकारक की प्रारंभिक सांद्रता है, x अभिकृत अभिकारक की सांद्रता है और t समय है)
View Solutionयदि हाइड्रोजन परमाणु की प्रथम कक्षा की त्रिज्या r1 है, तब r1 के पदों में द्वितीय, तृतीय और चतुर्थ कक्षाओं की त्रिज्या हैं:
View Solutionएक विलयन के लिए क्वथनांक में उन्नयन dTb तथा विलयन की मोललता (m) निम्न प्रकार संबंधित है: dTb=[RT2bΔHvap][M11+mM1],
जहां M1 विलायक का मोलर द्रव्यमान है और ΔHवाष्पन , विलायक के वाष्पन की ऊष्मा है। तनु विलयन के लिए, संबंध (dTbdm)m→0 प्रदर्शित करता है-
View Solutionयदि A और B के दो अणुओं का द्रव्यमान क्रमश: 100 amu और 64 amu है और A की विसरण दर 12xx10^(-3) है, तो B की विसरण दर क्या होगी?
View Solutionप्रबल अम्ल और प्रबल क्षार के उदासीनीकरण की मानक एन्थैल्पी –57.3 kJ "equiv"^(-1) है, यदि जलीय H_2S के प्रथम प्रोटॉन के उदासीनीकरण की एन्थैल्पी –33.7 kJmol^(-1) है, तब H_2S के लिए (pK_a)_1 है
View Solutionजब AX और BX2 के जलीय विलयन के माध्यम से विद्युत् के कूलॉम की बराबर संख्या प्रवाहित की जाती है और यदि A और B के निक्षेपित मोलों की संख्या क्रमशः Y और Z है तब-
View Solutionनिम्नलिखित अभिक्रियाओं के लिए k_s " और " k_e क्रमशः प्रतिस्थापन और विलोपन के लिए दर स्थिरांक हैं और mu = k_s/k_e है, सही विकल्प है
View Solutionदो क्रमागत कक्षाओं में इलेक्ट्रॉन के कोणीय संवेग का अनुपात a (a gt 1) है और उनका अंतर b है। तब (a)/(b) के बराबर है -
View Solutionयदि x1,x2 और x3 क्रमश: H - H, O = O और O - H बंध की एन्थैल्पी हैं, और x4 जल के वाष्पीकरण की एन्थैल्पी है, तब हाइड्रोजन के दहन की मानक एन्थैल्पी का आकलन कीजिए।
View Solution
