निकाय का प्रारंभिक विन्यास चित्र में दिखाया गया है।
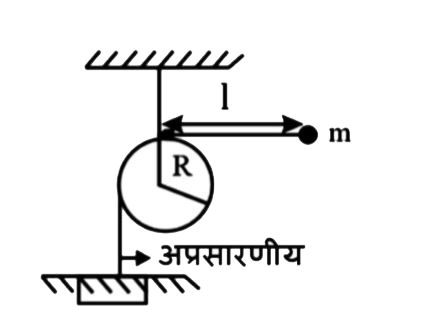
डोरी और घिरनी हल्की हैं। गोलक को मुक्त किया जाता है और डोरी घिरनी के चारों ओर लिपटना शुरू कर देती है। (घिरनी केंद्र पर अनुप्रयुक्त बल द्वारा स्थान पर रखी जाती है)
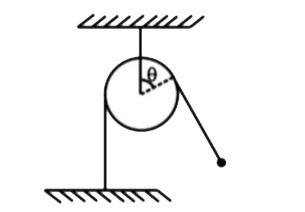
वह दर r ज्ञात कीजिए जिससे घिरनी के चारों ओर लपेटी गई डोरी की लंबाई बढ़ती ( के फलन के रूप में) है।
The correct Answer is:D
किसी भी क्षण, घिरनी पर लपेटी गई डोरी की लंबाई है और शेष लंबाई
दर है, जहाँ v कण की चाल है ऊँचाई, जिसके माध्यम से कण नीचे आता है
इसलिए,
Topper's Solved these Questions
Similar Questions
सोडियम प्रकाश के लिए, λ1 और λ2 तरंगदैर्यों पर दो पीली रेखाएं प्राप्त होती हैं। यदि इन दोनों का माध्य 6000Å और |λ2−λ1|=6Å है, तब λ1 और λ2 के संगत दो स्तरों के मध्य ऊर्जा अंतर लगभग है:
View Solutionसमरूप वृताकार गुहिकाओं के साथ दो समरूप एकसमान चक्तियो का एक निकाय चित्र में दिखाया गया है चित्र में विभिन्न सुसंगत निर्देशांक दिए गए है निकाय के दृव्यमान केंद्र के निदेशक है
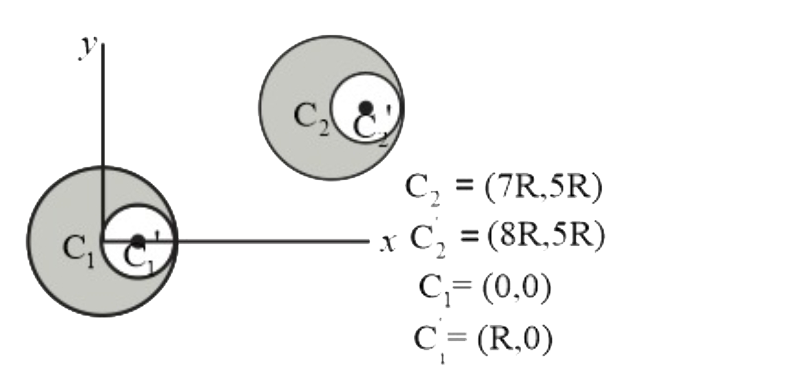
View Solutionएक कम्पनी दो प्रकार के टेलीफोनों का निर्माण करती है|पहला डोरी युक्त,दूसरा डोरी रहित| डोरी युक्त टेलीफ़ोन के निर्माण में 2 घंटे लगते है तथा रहित डोरी मॉडल के निर्माण में 4 घंटे लगते है| कम्पनी के पास इन प्रतिरूपों के निर्माण के लिए प्रतिदिन अधिक से अधिक 800 कार्य घंटे उपलब्ध है तथा पैकिंग विभाग प्रतिदिन अधिक से अधिक 300 टेलीफ़ोन सेटों को पैक कर सकता है|यदि कम्पनी डोरी युक्त मॉडल को रु 300 में बेचती है तथा डोरी रहित मॉडल को रु 400 में बचती है ,तो उसे प्रत्येक प्रकार के कितने टेलीफ़ोन सेल प्रतिदिन निर्मित करने चाहिए जिससे की उसकी बिक्री अधिकतम हो?
View Solutionनिम्नलिखित प्रश्नों के उत्तर लिखिए-
तोप के लिए 'धर रखी गई है' वाक्यांश का प्रयोग क्यों किया गया है?
View Solutionघिरनी निकाय |स्प्रिंग बल
View Solutionरस्सी में तनन |घिरनी निकाय
View Solutionप्रत्येक राष्ट्र की अपनी सांस्कृतिक धरोहर होती है जिसके बल पर वह प्रगति के पथ पर अग्रसर होता रहता है। मानव युग-युग से अपने जीवन को अधिक सुखमय, उपयोगी, शांतिमय और आनन्दपूर्ण बनाने का प्रयास कर रहा है। इस प्रयास का आधार वह सांस्कृतिक धरोहर होती है जो प्रत्येक मानव को विरासत के रूप में मिलती है. और इस प्रयास के फलस्वरूप मानव अपना विकास करता है। यह विकास सांस्कृतिक आधार के बिना संभव नहीं है। सभ्यता और संस्कृति दो अलग-अलग चीजें हैं। यद्यपि दोनों में गहरा रिश्ता है किन्तु संस्कृति मनुष्य को श्रेष्ठ और उन्नत बनाने की साधनाओं का नाम है और सभ्यता उन साधनाओं के फलस्वरूप उपलब्ध हुई जीवन प्रणाली का नाम है। सभ्यता के अन्तर में बहने वाली विचारधारा को हम संस्कृति कहते हैं जिसमें युगों से मानव-विकास के बीज विद्यमान हैं। किसी राष्ट्र का मूल्यांकन हम उसकी संस्कृति के आधार पर भी कर सकते हैं।
संस्कृति मनुष्य को श्रेष्ठ और_______ बनाने की साधनाओं का नाम है।
View Solutionप्रत्येक राष्ट्र की अपनी सांस्कृतिक धरोहर होती है जिसके बल पर वह प्रगति के पथ पर अग्रसर होता रहता है। मानव युग-युग से अपने जीवन को अधिक सुखमय, उपयोगी, शांतिमय और आनन्दपूर्ण बनाने का प्रयास कर रहा है। इस प्रयास का आधार वह सांस्कृतिक धरोहर होती है जो प्रत्येक मानव को विरासत के रूप में मिलती है. और इस प्रयास के फलस्वरूप मानव अपना विकास करता है। यह विकास सांस्कृतिक आधार के बिना संभव नहीं है। सभ्यता और संस्कृति दो अलग-अलग चीजें हैं। यद्यपि दोनों में गहरा रिश्ता है किन्तु संस्कृति मनुष्य को श्रेष्ठ और उन्नत बनाने की साधनाओं का नाम है और सभ्यता उन साधनाओं के फलस्वरूप उपलब्ध हुई जीवन प्रणाली का नाम है। सभ्यता के अन्तर में बहने वाली विचारधारा को हम संस्कृति कहते हैं जिसमें युगों से मानव-विकास के बीज विद्यमान हैं। किसी राष्ट्र का मूल्यांकन हम उसकी संस्कृति के आधार पर भी कर सकते हैं।
सांस्कृतिक धरोहर प्रत्येक मानव को- के रूप में मिलती है।
View Solutionप्रत्येक राष्ट्र की अपनी सांस्कृतिक धरोहर होती है जिसके बल पर वह प्रगति के पथ पर अग्रसर होता रहता है। मानव युग-युग से अपने जीवन को अधिक सुखमय, उपयोगी, शांतिमय और आनन्दपूर्ण बनाने का प्रयास कर रहा है। इस प्रयास का आधार वह सांस्कृतिक धरोहर होती है जो प्रत्येक मानव को विरासत के रूप में मिलती है. और इस प्रयास के फलस्वरूप मानव अपना विकास करता है। यह विकास सांस्कृतिक आधार के बिना संभव नहीं है। सभ्यता और संस्कृति दो अलग-अलग चीजें हैं। यद्यपि दोनों में गहरा रिश्ता है किन्तु संस्कृति मनुष्य को श्रेष्ठ और उन्नत बनाने की साधनाओं का नाम है और सभ्यता उन साधनाओं के फलस्वरूप उपलब्ध हुई जीवन प्रणाली का नाम है। सभ्यता के अन्तर में बहने वाली विचारधारा को हम संस्कृति कहते हैं जिसमें युगों से मानव-विकास के बीज विद्यमान हैं। किसी राष्ट्र का मूल्यांकन हम उसकी संस्कृति के आधार पर भी कर सकते हैं।
किसका विकास सांस्कृतिक आधार के बिना संभव नहीं है?
View Solutionएक व्यक्ति पश्चिम दिशा की ओर मूँह करके खड़ा है | वह दक्षिणावर्त दिशा में 45∘ के कोण पर घूमता है फिर वह पुनः उसी दिशा में 180∘ के कोण पर घूमता है और फिर वह वामावर्त दिशा में 270∘ के कोण पर घूमता है | अब वह किस दिशा की ओर खड़ा है ?
View Solutionघिरनी पर महत्वपूर्ण प्रश्न
View Solutionघिरनी त्वरित पर प्रश्न
View Solutionक्लोरीन गैस को MnO_2 और NaCl के साथ H_2SO_4 की अभिक्रिया द्वारा निर्मित किया जाता है। यदि अभिक्रिया में 50 g NaCl का उपयोग किया जाता है, तो STP पर Cl_2 के कितने आयतन का निर्माण होगा?
View SolutionCIF_4^(+) में केंद्रीय रूप के चारों ओर की आकृति है:
View Solutionसंगलित अशुद्ध धातु को लकड़ी के हरे रंग के लट्टे के साथ हिलाकर फफोलेदार तांबा को परिष्कृत किया जाता है, क्योंकि इस प्रकार की लकड़ी, हाइड्रोकार्बन गैसों (जैसे CH_4 ) को मुक्त करती है। इस प्रक्रम X को ________ कहा जाता है और इसका उपयोग धातु में प्रारंभ में उपस्थित Y की अशुद्धियों के शुद्धिकरण के लिए किया जाता है। Y _______ है।
View Solutionनाइट्रोजन युक्त कार्बनिक यौगिक के 29.5 mg को केल्डॉल विधि द्वारा उपचारित किया जाता है और मुक्त अमोनिया को 0.1 M HCI विलयन के 20mL में अवशोषित किया जाता है। अम्ल के आधिक्य के पूर्ण उदासीनीकरण के लिए 0.1M NaOH विलयन के 15mL की आवश्यकता होती है। यौगिक में नाइट्रोजन की प्रतिशतता है
View Solution
