400 Hz आवृत्ति की ध्वनि उत्सर्जित करने वाला एक ध्वनि स्रोत S तथा m द्रव्यमान का एक ग्राही R समान बिंदु पर हैं। R बल नियतांक K की स्प्रिंग की सहायता से सरल आवर्त गति कर रहा है। समय t = 0 पर, R माध्य स्थिति में है और दाहिनी ओर गतिशील है, जैसा कि दर्शया गया है। उसी समय, स्रोत कुछ त्वरण a के साथ R से दूर जाने लगता है। ग्राही द्वारा एक समय t = 10 s में, पंजीकृत की गई आवृत्ति 250 Hz है। वह समय (सेकंड में) क्या है, जिस पर स्रोत द्वारा 250 Hz की संगत पंजीकृत आवृत्ति को उत्सर्जित किया गया था? [दिया गया है कि और दोलन का आयाम ]

The correct Answer is:8
दोलन का आवर्तकाल इस प्रकार, t = 10 s पर, ग्राही दाईं ओर माध्य स्थिति से के वेग से गुजरता है।
डॉप्लर के सूत्र का उपयोग करके
तो तरंग का वेग है, जो t= 10 s पर तरंग के उत्सर्जन का समय जिसे ग्राही द्वारा प्राप्त किया गया है, माना T वह समय है जब तरंग उत्सर्जित हुई, तो ग्राही से तरंग की दूरी , है। यह दूरी 10 - T समय में तरंग द्वारा तय की जाती है। इसलिए,
Topper's Solved these Questions
Similar Questions
हाइड्रोजन परमाणु में एक इलेक्ट्रॉन n = 2 से n = 1 तक एक संक्रमण करता है और एक फोटॉन का उत्सर्जन करता है। यह फोटॉन एक द्विआयनित लीथियम परमाणु से टकराता है जो पहले से ही एक उत्तेजित अवस्था में था और परिक्रमण करने वाले इलेक्ट्रॉन को पूर्णतः बाहर निकाल देता है। प्रक्रम के लिए लीथियम-आयन की उत्तेजित अवस्था के लिए न्यूनतम क्वांटम संख्या है:
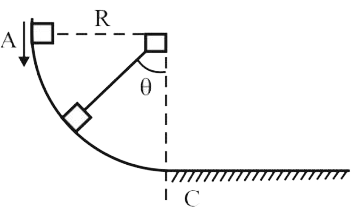
View Solutionद्रव्यमान m का एक गुटका एक ऊर्ध्वाधर स्थिर वृत्ताकार पथ पर रखा गया है और फिर इसे पथ पर स्थिति A पर पथ के अनुदिश v वेग दिया जाता है। गुटके और पथ के बीच घर्षण गुणांक कोण के साथ परिवर्तित होता है। यदि गुटका स्थिर चाल के साथ पथ पर गति करता है तो घर्षण गुणांक क्या है?
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionएक कण y=x2+2x से साथ-साथ चलता है। व्रक के किस बिंदु पर x तथा y निर्देशांक समान दर से परिवर्तित हो रहे है ?
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionएक थैले में 3 सफेद और 5 काली गेंदें हैं। थैले के अंदर से बिना देखे एक गेंद निकाली जाती है।
(a) एक सफेद गेंद प्राप्त करने की प्रायिकता क्या है?
(b) एक काली गेंद प्राप्त करने की प्रायिकता क्या है?
View SolutionThe distance between 2 places R and S is 42 km. Anita starts from R with a uniform speed of 4km/h towards S and at the same time Romita starts from S towards R also with same uniform speed. They meet each other after 6 hours. The speed of Romita is दो स्थान R और S के बीच की दूरी 42 किमी है। अनीता R से S की और 4 किमी/घंटा की एक समान गति से चलना शुरू करती है ओर ठीक उसी समय रोमिता S से R की ओर एक समान गति से चलना शुरू करती हे। वे 6 घंटे के बाद एक दूसरे से मिलते हैं। रोमिता को गति कितनी है?
View Solution30 बच्चो की एक कक्षा में सरन शीर्ष से 9 वे रैंक पर है| मनीष सरन से पांच रैंक निचे है| तल से मनीष की रैंक क्या है?
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View SolutionAlok starts walking from P with speed of 6 km/h towards Q. Raman starts at same time from P towards Q with speed of 9 km/h. Raman reaches Q, turns back and starts walking towards P. He meets Alok at R. If PQ is 15 km, then what is PR?
आलोक P बिंदु से Q की ओर 6 km/h की गति से चलना शुरू करता है। रमन 9 km/h की गति के साथ P से की Q की ओर चलना आरम्भ करता है। रमन Q पर पहुँचता है, वापस मुड़ता है और P की ओर चलना शुरू कर देता है। वह आलोक से R पर मिलता है। यदि PQ 15 km है, तो PR कितना है?
View Solutionदेवनागरी लिपि के सन्दर्भ में कौन-से कथन सत्य है?
I. देवनागरी में एक ध्वनि के लिए एक ही प्रतीक है।
II. देवनागरी में विदेशी ध्वनियों को व्यक्त करने की क्षमता है।
III. देवनागरी दाई ओर से बाईं ओर लिखी जाती है।
IV. देवनागरी में वर्णों की संख्या रोमन लिपि से कम है।
View SolutionA group of 6 members is sitting in a row. Ram is to the left of Shyam and right of Sita who is to the right of Raman and Suman is to the right of Ravi who is to the left of Raman. Which of the members are sitting in the centre ? छः सदस्यों का एक दल एक पंक्ति में बैठा है। राम की स्थिति श्याम के बाईं ओर है और सीता के दाहिनी ओर, जो स्वयं रमण के दाहिनी ओर है और सुमन की स्थिति रवि के दाहिनी ओर, जो स्वयं रमण के बाईं ओर है। कौन-से सदस्य ठीक बीचों-बीच बैठे हैं?
View Solutionनाभिक से दूरी पर, अनंतसूक्ष्म मोटाई dr के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4rr2 dr है। r पर P की निर्भरता का गुणात्मक रेखाचित्र है-
View Solutionएक एंजाइम उत्प्रेरित अभिक्रिया के लिए, ताप (T) के सापेक्ष अभिक्रिया की दर (r) को आलेखित किया गया है। निम्नलिखित में से कौन सा सही निरूपण है?
View Solution
