YDSE में, झिर्रियों की चौड़ाई अलग-अलग है। परिणामस्वरूप, दो झिर्रियों से तरंगों के आयाम क्रमश: A और 2A हैं। यदि व्यतिकरण पैटर्न की अधिकतम तीव्रता I0 हो तो एक बिंदु जहाँ तरंगों के बीच कलांतर ϕ है, पर पैटर्न की तीव्रता I0P(5+4cosϕ) के द्वारा दी जाती है। जहाँ P पूर्णांक है। P का मान ज्ञात कीजिए।
9
3
6
1
The correct Answer is:A
चूँकि आयाम A और 2A हैं तो तीव्रताओं का अनुपात 1:4 है
Iअधिकतम=I0=I1+I2+2√I1×I2=I+4I+2×2I
I0=9I⇒I=I09
किसी भी बिंदु पर तीव्रता:
I.=I1+I2+2√I1×I2cosϕ
I.=I+4I+2√I×4Icosϕ
I.=5I+4Icosϕ,I.=I[5+4cosϕ]
I.=I09[5+4cosϕ]=I0P[5+4cosϕ]
P=9
Topper's Solved these Questions
- JEE-MAIN TEST - 51BOOK - NTA MOCK TESTSCHAPTER - JEE-MAIN TEST - 51EXERCISE - भौतिक विज्ञान(विषयपरक आंकिक)
5 Videos
- JEE-MAIN TEST - 38 BOOK - NTA MOCK TESTSCHAPTER - JEE-MAIN TEST - 38 EXERCISE - भौतिक विज्ञान(विषयपरक आंकिक)
5 Videos
- JEE-MAIN TEST -61BOOK - NTA MOCK TESTSCHAPTER - JEE-MAIN TEST -61EXERCISE - भौतिक विज्ञान
25 Videos
Similar Questions
1 kg द्रव्यमान का एक गुटका μ=1√3 के एक खुरदरे आनत तल के शीर्ष से मुक्त किया जाता है। गुटके की प्रारंभिक चाल 2ms−1 है। चित्र के अनुसार नियतांक k=1Nm−1 की एक स्प्रिंग अज्ञात लंबाई के आनत तल के आधार से जुड़ी हुई है। स्प्रिंग का अधिकतम संपीडन ज्ञात कीजिए ।(उत्तर मीटर में दीजिए)।
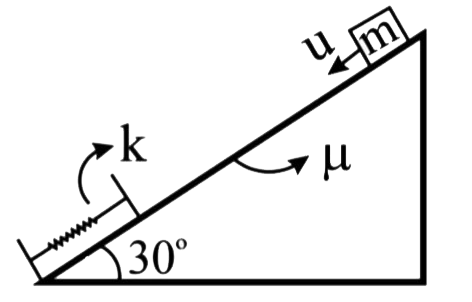
View Solutionm द्रव्यमान की एक गेंद, जो v वेग से गतिमान है, विरामावस्था में एक लोलक के गोलक से टकराती है। गोलक का द्रव्यमान भी m है। यदि संघट्ट पूर्णतः अप्रत्यास्थ है, जिस ऊंचाई तक गोलक ऊपर जाएगा, h=v2x⋅g द्वारा दी जाती है, तो x का मान है:
View Solutionबोर मॉल के अनुसार एक द्वि आयनित Li परमाणु (Z=3) की मूल अवस्था से एक इलैक्ट्रॉन को निकालने के लिए आवश्यक न्यूनतम ऊर्जा (eV में ) है
View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
View Solutionबिंदु P,Q,R,S के निर्देशांक (2,a),(3,5),(3,4)और (0,6) है । यदि रेखा PR लंबवत हो QS पर तो a का मान ज्ञात कीजिए ।
View Solutionदो स्थिर बिंदु A और B के निर्देशांक क्रमशः (a,0) और (−a,0) है , तो चर बिंदु P का बिन्दुपथ ज्ञात कीजिए जबकि :
PA=nPB , जहाँ n अचर है ।
View Solutionएक छोटी फर्म सोने के अंगूठियां और चेनों का निर्माण करती है| प्रतिदिन अंगूठियों और चेनों के निर्माण की कुल संख्या अधिकतम 24 है| एक अंगूठी बनाने में एक घंटा तथा के चेन के बनाने में 30 मिनट लगते है| प्रतिदिन उपलब्ध घंटों की अधिकतम संख्या 16 है|यदि अंगूठी पर लाभ रु 300 तथा एक चेन पर लाभ रु 190 हो, तो ज्ञात कीजिए| की प्रतिदिन कितनी अंगूठियों और चेनों का निर्माण किया जाय ताकि अधिकतम लाभ कमाया जा सकें|
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए , जिसके निर्देशांक है :
x=asecϕ,y=btanϕ, जहाँ ϕ चर है ।
View SolutionA और B दो स्थिर बिंदु है जिनके निर्देशांक क्रमश : (a,0) और (−a,0) है । चर बिंदु P के बिन्दुपथ का समीकरण ज्ञात कीजिए , जबकि
PA+λPB=0 , जहाँ λ कोई अचर है ।
View SolutionA और B दो स्थिर बिंदु है जिनके निर्देशांक क्रमश : (a,0) और (−a,0) है । चर बिंदु P के बिन्दुपथ का समीकरण ज्ञात कीजिए , जबकि
PA+PB=c, जहाँ c कोई अचर है ।
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
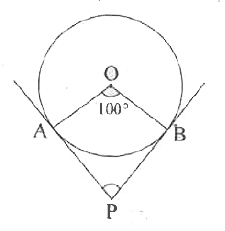
View Solutionयदि शब्द PROBABILITY के अक्षर एक पंक्ति में यदृच्छया लिखे जाते है तो दो के साथ आने की प्रायिकता है -
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionबिंदु P की बिंदु (4,3) से दूरी √10 है। बिंदु P के निर्देशांक ज्ञात कीजिए यदि इस की कोटि भुज से दुगुनी हो।
View Solution
