एक रोटर में एक खोकली उधारवाधर बेलनाकार सरचना अपनी अक्ष के पारित घूमती है और एक व्यक्ति आंतरिक दिवार के सहांरे खड़ा है व्यक्ति की एक विशिस्ट चाल पर व्यक्ति के निचे के फर्श को हटा दिया जाता है और व्यक्ति बिना किसी फर्श के दिवार के सहारे लटकता है यदि रोटर की त्रिज्या 2 m है और दिवार और व्यक्ति के बिच स्थिर घर्षण गुणांक 0.2 है तब दिवार की न्यूनतम चाल (ms−1) ज्ञात कीजिए जिस पर फर्श को हटाया जा सकता है
स्थिति को आरेख में दिखाया गया है
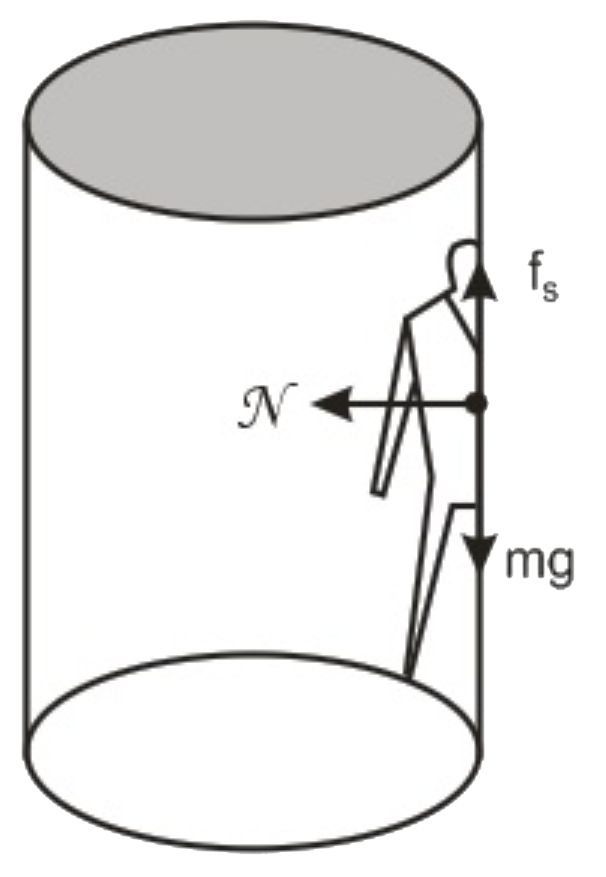
जब फर्श को हटा दिया गया है तब व्यक्ति पर लगने वाले बल है
1 .भार mg निचे की और है
2. दिवार के कारन अभिलम्ब बल N केंद्र की और है
3. घरसँ बल fS दिवार के समान्तर और ऊपर की और है
व्यक्ति एकसमान चाल के साथ एक वृत्त में घूम रहा है इसलिए इसका त्वरण केंद्र की और है क्षैतिज दिशा के लिए नेव्तोन का नियम (दूसरा नियम ) और उध्र्वाधर दिशा के लिए नेव्तोन का नियम (पहला नियम ) देता है
N=mv2/r.....(i)
fs=mg.....(ii)
न्यूनतम चाल के लिए जब फर्श हटाया जा सकता है तो घर्सन सीमांत है और इसलिए यह μsN के बराबर है इससे हमें प्राप्त होता है
μsN=mg या μsmv2r=mg
या v=√rgμs=√2m×10m/s20.2
=10ms−1
Topper's Solved these Questions
Similar Questions
इलेक्ट्रान a कण और प्रोटीन की दी ब्रोग्ली तरंग धैर्य सभी में समान गतिज ऊर्जा होती है जो करमस λe,λaऔर λp के रूप में दी जाती है तो निम्नलिखित में से कोनसा सही नहीं है
View Solutionलाइमैन श्रेणी में पहली रेखा की तरंगदैर्ध्य λ है। बामर श्रेणी में प्रथम रेखा की तरंगदैर्ध्य है:
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। प्रायिकता ज्ञात कीजिए कि 5 कदम चलने के पश्चात, यह व्यक्ति प्रारम्भिक बिन्दु से एक कदम दूर है।
View Solutionमुक्तिबोध की कविता आधुनिक जागरूकं व्यक्ति के -की कविता है।
View Solutionएक व्यक्ति पश्चिम दिशा की ओर मूँह करके खड़ा है | वह दक्षिणावर्त दिशा में 45∘ के कोण पर घूमता है फिर वह पुनः उसी दिशा में 180∘ के कोण पर घूमता है और फिर वह वामावर्त दिशा में 270∘ के कोण पर घूमता है | अब वह किस दिशा की ओर खड़ा है ?
View SolutionSeven professionals are standing in a row. A journalistis to the immediate right of a pharmacist and to the immediate left of a teacher. An advocate is on the immediate right of an accountant . The advocate and pharmacist have one person between them .The teacher and a doctor have two persons between them, an architect and the pharmacist have two persons between them . Who is in the middle? सात पेशेवर एक पंक्ति में खड़े हैं। एक फार्मासिस्ट के तत्काल दाईं ओर एक पत्रकार और एक शिक्षक के तत्काल बाईं ओर है। एक वकील एक एकाउंटेंट के तत्काल दाईं ओर है। अधिवक्ता और फार्मासिस्ट के बीच एक व्यक्ति है। शिक्षक और डॉक्टर के बीच दो व्यक्ति हैं। आर्किटेक्ट और फार्मासिस्ट बीच में दो व्यक्ति होते हैं। बीच में कौन है?
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solutionएक धातु वायु के आधिक्य में दहन करने पर X निर्मित करती है। जल के साथ जल अपघटन पर X,H_(2)O_(2) और O_(2) के साथ एक और उत्पाद निर्मित करता है। धातु कौन सी है?
View Solutionएक आदर्श गैस के दस मोलों को एक बंद पात्र में भरा जाता है । पात्र में बेलन और पिस्टन के प्रकार की व्यवस्था है और 0.821 atm पर गैस का दाब स्थिर रहता है। निम्नलिखित में से कौन सा आलेख logV और logT के परिवर्तन का सही निरूपण करता है? (V= आयतन(लीटर में) और T= ताप (केलिवन में)
View SolutionNaCl के संकुलन प्रभाज के लिए निम्नलिखित में से कौन सा व्यंजक सही है, यदि एक फलक और एक विकर्ण से a- आयन को हटा दिया जाता है?
View SolutionNaCl संरचना वाले एक ठोस AB में, 'A' परमाणु धन एकक कोष्ठिका के कोनो और फलक केंद्र पर स्थित होते है | यदि एक अक्ष के अनुदिश सभी फलक केन्द्रित पर्मानुओ को हटा दिया जाता है, तो ठोस की परिणामी रससमीकरणमिति होगी:
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solutionयदि हाइड्रोजन और ऑक्सीजन को मिश्रित किया जाता है और कमरे के ताप पर, एक ही पात्र में रखा जाता है, तब जल के निर्माण के लिए अभिक्रिया नहीं होती है क्योकिं:
View Solutionएक बंद पात्र में कार्बन मोनोऑक्साइड के 2 मोल और ऑक्सीजन के 1 मोल के मिश्रण को कार्बन डाइऑक्साइड प्राप्त करने के लिए प्रज्वलित किया जाता है, तब
View Solutionकमरे के ताप पर, एक जलीय मिश्रण अमोनियम क्लोराइड के संबंध में 0.1 M और NH4OH के संबंध में 0.01 M है। एक क्षार के रूप में जलीय अमोनिया का pKb=5 है। मिश्रण की pH लगभग है-
View Solution
