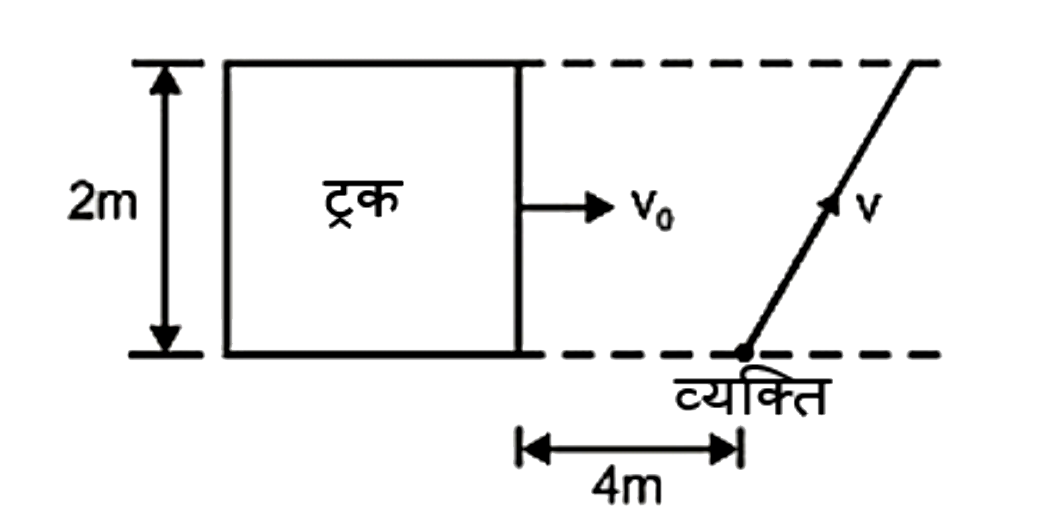
एक 2m चौड़ा ट्रक एक सीधे क्षैतिज मार्ग के अनुदिश की एकसमान चाल से गतिशील है। एक पैदल यात्री एक समान चाल v से एक सीधी रेखा में चलते हुए सड़क को पार करना प्रारंभ करता है जब ट्रक उससे 4m दूर होता है। तब v का न्यूनतम मान क्या होगा ताकि वह सुरक्षित रूप से सड़क पार कर सकें?
The correct Answer is:C
आकृति में दर्शाये गए अनुसार माना व्यक्ति कोण पर सड़क को पार करना प्रारंभ करता है तथा सुरक्षित पार करने केलिए शर्त यह है की व्यक्ति को उस समय तक सड़क पार कर लेना चाहिए जब तक कि ट्रक या दूरी का तय न कर लें।
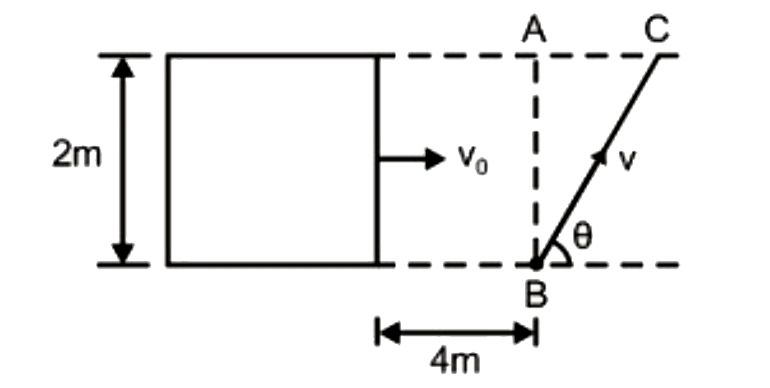
या .......i
न्यूनतम v के लिए
या
या
या
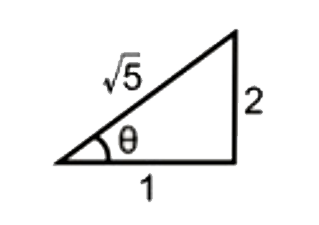
समीकरण 1 से
Topper's Solved these Questions
Similar Questions
प्रथम उत्तेजित अवस्था में एक स्थिर हाइड्रोजन परमाणु एक फोटॉन उत्सर्जित करता है। यदि हाइड्रोजन परमाणु का द्रव्यमान m है और इसकी आयनन ऊर्जा E है तब परमाणु द्वारा उत्सर्जित प्रतिक्षेप वेग है [प्रकाश की चाल =c]
View Solutionएक क्षैतिज चकती अपने केंद्र से गुजरने वाली एक ऊर्ध्वाधर अक्ष के परितः ω कोणीय वेग के साथ घूर्णन कर रही है। एक गेंद को खांचे के केंद्र में रखा जाता है और थोड़ा धक्का दिया जाता है। गेंद का वेग जब यह खांचे से बाहर आती है:
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
View Solutionएक थैले में 3 सफेद और 5 काली गेंदें हैं। थैले के अंदर से बिना देखे एक गेंद निकाली जाती है।
(a) एक सफेद गेंद प्राप्त करने की प्रायिकता क्या है?
(b) एक काली गेंद प्राप्त करने की प्रायिकता क्या है?
View SolutionA 360 m long train running at a uniform speed, crosses a platform in 55 seconds and a man standing on the platform in 24 seconds. What is the length (in metre) of the platform?
360 मी लंबी एक ट्रेन एक समान चाल से चलते हुए किसी प्लेटफ़ॉर्म को 55 सेकंड में तथा प्लेटफ़ॉर्म पर खड़े एक व्यक्ति को 24 सेकंड में पार करती है | प्लेटफ़ॉर्म की लंबाई ( मीटर में ) कितनी है ?
View SolutionA train travels at a speed of 76 km/hr. If it crosses a pole in 36 sec. The length of the train is:
एक ट्रेन 76 किमी/घंटा की चाल से चलती है | यदि यह एक खंभे को 36 सेकंड में पार करती है, तो ट्रेन की लंबाई क्या है ?
View Solutionविरंजक चूर्ण में इसके एक घटक के रूप में एक ऑक्सोअम्ल का लवण होता है। इस अम्ल का एनहाइड्राइड है:
View Solutionएक क्षार का मेथिल ऑरेंज को सूचक के रूप में उपयोग करते हुए एक अम्ल के साथ अनुमापन किया जाता है। निम्नलिखित में से कौन सा एक सही संयोजन है?
View Solutionनिम्नलिखित में से कौन सा कथन सही है? 1. एक sigma बंध एक pi बंध से प्रबल होता है 2. एक सहसंयोजक बंध एक हाइड्रोजन बंध से प्रबल होता है 3. HE, HCI से अधिक ध्रुवीय होता है 4. मेथिलीन क्लोराइड में एक विद्युत् संयोजक बंध और तीन सहसंयोजक बंध होते हैं नीचे दिए गए कोड का उपयोग करके सही उत्तर का चयन कीजिए।
View Solutionनिम्नलिखित में से किस औषधि का उपयोग एक पीड़ाहारी के रूप में किया जाता है?
View Solutionसंगमरमर निम्नलिखित में से किसके लिए एक सिंक के रूप में कार्य करता है?
View Solutionनिम्नलिखित में से कौन-सा हैलोजन एक से अधिक ऑक्सोअम्ल का निर्माण नहीं कर सकता है?
View Solutionनिम्नलिखित में से कौनसी अभिक्रिया में हाइड्रोजन परॉक्साइड, एक ऑक्सीकारक के रूप में कार्य करता है?
View Solutionनिम्नलिखित में से कौनसी एल्कोहॉल की एक विशेषता नहीं है?
View Solution
