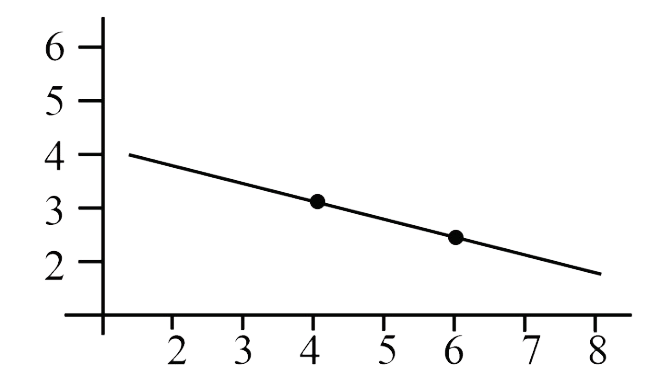
एक रेडियोसक्रिय तत्व की अर्ध-आयु निर्धारित करने के लिए, एक छात्र,ln∣∣∣dN(t)dt∣∣∣ बनाम t का आलेख खींचता है। यहाँ dN(t)dt , समय t पर रेडियोसक्रिय क्षय की दर है। यदि इस तत्व के रेडियोसक्रिय नाभिकों की संख्या, 4. 16 वर्ष के बाद p के गुणक से घट जाती है, तो p का मान है:
8
7
4
8.5
The correct Answer is:A
∣∣∣dNdt∣∣∣ = रेडियोसक्रिय पदार्थ की सक्रियता
=λN=λN0e−λt(∴N=N0e−λt)
दोनों पक्षों का लघुगणक लेने पर,
ln∣∣∣dNdt∣∣∣=ln(λN0)−λt
अतः, In∣∣∣dNdt∣∣∣ बनाम t आलेख, प्रवणता - λ के साथ एक सरल रेखा है।
आलेख से, हम देख सकते हैं कि,
λ=12=0.5 प्रति वर्ष
अब समीकरण लागू करने पर,
N=N0e−λt=N0e−0.5×4.16
=N0e−2.08=N0e−2×(0.693)=0.125N0
=N08
अर्थात, नाभिक, 8 के गुणक से घटते हैं।
अतः, उत्तर 8 है।
Topper's Solved these Questions
Similar Questions
कुछ उत्तेजित अवस्था A में हाइड्रोजलन सद्रश उदासीन नमूने, ऊर्जा 3.066eV के एक फोटॉन को अवशोषित करके, एक नई अवस्था B मे उत्तेजित हो जाती है। जब अवस्था B से इलेक्रॉालन वापस लौटता है तो अधिकतम दस अलग अलग तरंगदैर्ध्य के फोटॉन देखें जा सकते हैं जिनमें कुछ फोटॉन 3.066 eV से कम ऊर्जा के है कुछ समान ऊर्जा के हैं और केवल चार फोटान 3.066eV से अधिक ऊर्जा वाले हैं तब इस परमाणु की आयनन ऊर्जा है:
View Solutionकल्पना कीजिए कि प्रोटॉन से बने परमाणु और इलेक्ट्रॉन के दोगुने द्रव्यमान का एक काल्पनिक कण, लेकिन आवेश इलेक्ट्रॉन के समान ही है। बोर परमाणु मॉडल को लागू कीजिए और प्रथम उत्तेजित स्तर पर इस काल्पनिक कण के सभी संभव संक्रमण पर विचार कीजिए। सबसे लंबी तरंग दैर्ध्य वाले फोटॉन की तरंग दैर्ध्य λ (हाइड्रोजन परमाणु के लिए रिडबर्ग नियतांक R के पदों में दिया गया है) बराबर है:
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionयदि पिता एवं पुत्र की आयु का योग (वर्षो में) 65 है तथा उनकी आयु के अन्तर का दुगुना 50 वर्ष है तब पिता की आयु होगी -
View Solutionरेडियोसक्रिय तत्व A का अर्ध आयु काल 10 दिन है। 1 मोल के साथ प्रारंभ होने पर 11वें दिन के अंत में A की शेष मात्रा (12)n+610 मोल है। n का मान क्या है?
View Solutionनाभिक से दूरी पर, अनंतसूक्ष्म मोटाई dr के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4rr2 dr है। r पर P की निर्भरता का गुणात्मक रेखाचित्र है-
View Solutionएक एंजाइम उत्प्रेरित अभिक्रिया के लिए, ताप (T) के सापेक्ष अभिक्रिया की दर (r) को आलेखित किया गया है। निम्नलिखित में से कौन सा सही निरूपण है?
View Solutionप्रथम कोटि अभिक्रिया के लिए निम्नलिखित में से कौन सा सही है/हैं? (a अभिकारक की प्रारंभिक सांद्रता है, x अभिकृत अभिकारक की सांद्रता है और t समय है)
View Solutionसिरोटोनिन एक प्रसिद्ध प्रशान्तक है। यदि इसमें एकाकी युग्म इलेक्ट्रॉनों की संख्या 'X' और T -बंधों की संख्या 'Y' है, तो x + Y का योगफल किसके बराबर है :
View Solutionउच्च तापमान पर एक साम्यावस्था क्रियाकारकां की ओर विस्थापित हो जाती है इस साम्यावस्था के लिए In K तथा 1//T के मध्य कौन सा आलेख सही है?
View Solutionसक्रियण ऊर्जा की गणना के लिए log k बनाम 1/T के बीच का आरेख किसके द्वारा दिखाया गया है?
View Solutionठोस पर, एक गैस के अधिशोषण के लिए, log (x/m) और log P का आलेख रेखिक है, जिसकी ढाल है: (n पूर्णांक संख्या है)
View Solutionशून्य कोटि की अभिक्रिया A rarr B + C के लिए, A की प्रारंभिक सांद्रता 0.1 M है। यदि 10 मिनट के बाद [A] = 0.08 M है, तो इसकी अर्ध आयु और पूर्ण होने का समय क्रमशः है:
View Solutionरेडियोएक्टिव ""^14C के क्षय के लिए अर्द्धआयु 5730 वर्ष है। लकड़ी की एक पुरातात्विक कलाकृति में ""^14C की सक्रियता, जीवित पेड़ों में पायी जाने वाली सक्रियता की 80% है। कलाकृति की आयु होगी: [दिया हुआ है: log 1.25 = 0.0969]
View Solutionएक अभिक्रिया 2A+B→ उत्पाद के लिए केवल B की सांद्रता को दोगुना करने पर दोगुनी हो जाती है और दोनों अभिकारकों की प्रारंभिक सांद्रता को दोगुना करने पर दर 8 गुना बढ़ जाती है। अभिक्रिया के लिएदर नियम है:
View Solution
