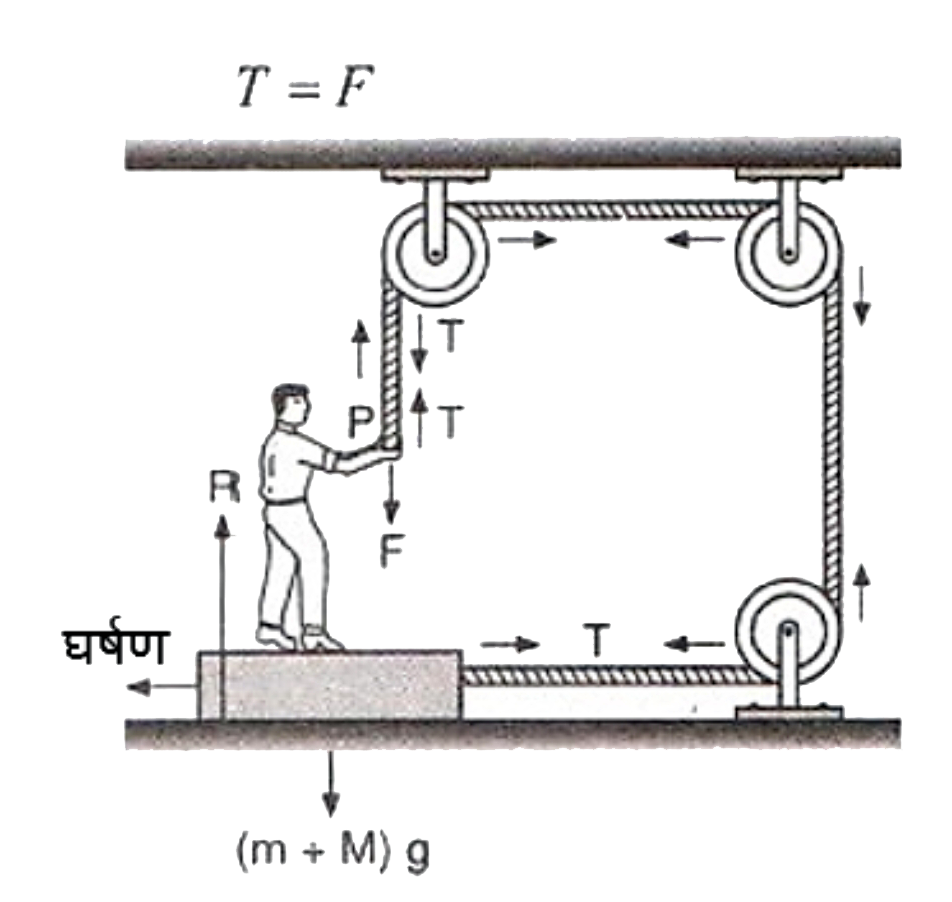
आरेख में दिखाए गए बोर्ड और फर्श के बीच घर्षण गुणांक μ है। अधिकतम बल ज्ञात कीजिए जो आदमी, रस्सी पर लगा सकता है, ताकि बोर्ड फर्श पर न फिसले।

μ(m+M)g(2+μ)
μ(m+M)g(1+μ)
μ(m+M)g(2−μ)
μ(m+M)g(1−μ)
The correct Answer is:B
निकाय पर कार्य करने वाले बलों को आरेख में दिखाया गया है
बिंद P के ऊर्ध्वाधर साम्यावस्था के लिए
T=F ...(i)
और निकाय की ऊर्ध्वाधर साम्यावस्था के लिए
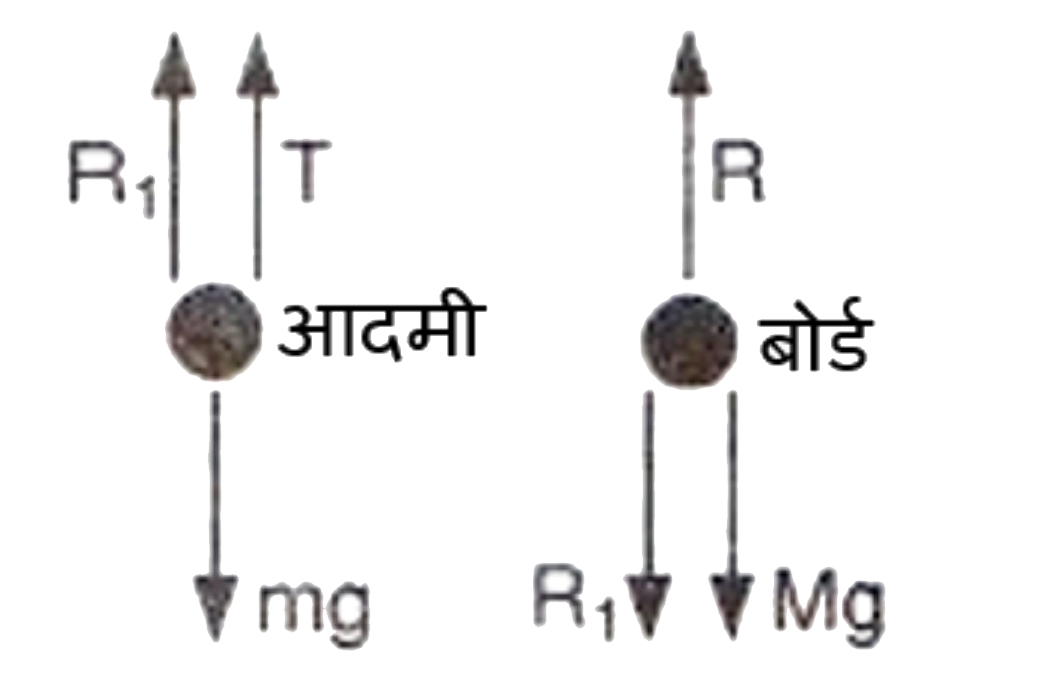
R+T=(m+M)g, अर्थात,
R=(m+M)g−T ...(ii)
अब निकाय क्षैतिज रूप से तब तक नहीं गति करेगा, जब तक
T<fL
अर्थात, T<μ[(m+M)g−T]
(fL=μR)
जो सरलीकरण करने पर, देता है
T<μ(m+M)g(1+μ)
इसलिए समीकरण (i) के प्रकाश में, हम प्राप्त करते हैं
Fmax=μ(m+M)g(1+μ)
Topper's Solved these Questions
- JEE MAIN TEST-58BOOK - NTA MOCK TESTSCHAPTER - JEE MAIN TEST-58EXERCISE - भौतिक विज्ञान(विषयपरक आंकिक)
5 Videos
- JEE MAIN TEST-40BOOK - NTA MOCK TESTSCHAPTER - JEE MAIN TEST-40EXERCISE - भौतिक विज्ञान
25 Videos
- JEE MAIN TEST-59BOOK - NTA MOCK TESTSCHAPTER - JEE MAIN TEST-59EXERCISE - भौतिक विज्ञान
25 Videos
Similar Questions
एक नाव 24 km प्रतिप्रवाह और 36 km अनुप्रवाह को 6 घंटे में तय करती है, जबकि यह 36 km प्रतिप्रवाह और 24 km अनुप्रवाह को 612 घंटे में तय करती है। धारा का वेग (kmph में) है:
View Solutionएकल आयनित हीलियम परमाणु से इलेक्ट्रॉन को निकालने के लिए आवश्यक ऊर्जा, हीलियम परमाणु से एक इलेक्ट्रॉन को निकालने के लिए आवश्यक ऊर्जा की 2. 2 गुनी है। हीलियम परमाणु को पूरी तरह से आयनीकृत करने के लिए आवश्यक कुल ऊर्जा किसके निकट है?
View Solutionv चाल से गतिमान एक हाइड्रोजन परमाणु विरामावस्था में स्थित दूसरे हाइड्रोजन परमाणु से संघट्ट करता है। v का न्यूनतम मान ज्ञात कीजिए जिसके लिए दोनों परमाणुओं में से एक आयनित हो सके। एक हाइड्रोजन परमाणु का द्रव्यमान =1.67×10−27 kg है। संघट्ट को पूर्णतः अप्रत्यास्थ मानिए।
View Solutionचित्र में प्रदर्शित ब्लॉकों के बीच घर्षण गुणांक μ है, किन्तु फर्श घर्षणरहित है|
View Solutionउन सरल रेखाओ के समीकरण ज्ञात कीजिए जो :
x=3 तथा x=−3 से समान दूरी पर है
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solutionएक छोटी फर्म सोने के अंगूठियां और चेनों का निर्माण करती है| प्रतिदिन अंगूठियों और चेनों के निर्माण की कुल संख्या अधिकतम 24 है| एक अंगूठी बनाने में एक घंटा तथा के चेन के बनाने में 30 मिनट लगते है| प्रतिदिन उपलब्ध घंटों की अधिकतम संख्या 16 है|यदि अंगूठी पर लाभ रु 300 तथा एक चेन पर लाभ रु 190 हो, तो ज्ञात कीजिए| की प्रतिदिन कितनी अंगूठियों और चेनों का निर्माण किया जाय ताकि अधिकतम लाभ कमाया जा सकें|
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionचित्र में दिखाए गए छायांकित क्षेत्र के लिए असामिका है-
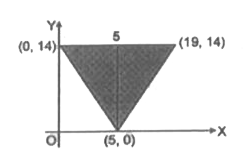
View Solutionबिंदुओं (3,1) और (0,y) के बीच की दूरी 5 है। y ज्ञात कीजिए।
View Solutionएक बिन्दु पर क्रियाशील दो बल P और Q का अधिकतम परिणामी बल ........ होता है।
View Solutionयू.पी. बोर्ड स्पेशल (आर्यभट्ट Revision Series)|समीकरणों के हल पर आधारित बोर्ड परीक्षा में आये हुए प्रश्नों पर चर्चा
View Solutionबोर्ड स्पेशल |द्विघात समीकरण का Revision #!#बोर्ड में पूछे गए सवालों पर चर्चा
View Solutionबोर्ड के लिए महत्वपूर्ण प्रश्नों पर चर्चा
View Solutionसमांतर श्रेणी के n पदों के योग पर प्रश्न |बोर्ड परीक्षा मे पूछे गए प्रश्न
View Solutionछत्तीसगढ़ , म०प्र०, राजस्थान , झारखंड तथा महाराष्ट्र बोर्ड स्पेशल |बोर्ड परीक्षा में त्रिभुज पर पूछे गए प्रश्नों को Discussion
View Solution
