समान अनुप्रस्थ काट और विभिन्न प्रतिरोधकतओं ρ1 और ρ2 के साथ दो बेलनाकार चालक सिरों से सटाकर रखे है। चालकों की परिसीमा पर आवेश ज्ञात कीजिए यदि एक धारा I चालक 1 से चालक 2 में प्रवाहित होती है।
ε0(ρ2−ρ1)l
ε0(2ρ2+ρ1)l
2ε0(ρ1−ρ2)l
ε0(ρ1+ρ2)l
The correct Answer is:A
ओम के नियम के अनुसार →E=ρ→J
प्रश्न निम्न चरणों द्वारा हल किया गया है
चरण I: दोनों चालकों में विद्युत क्षेत्र निर्धारित कीजिए। पहले चालक में धारा घनत्व है
J1=1nπR2 (चालक की लंबाई के अनुदिश)

इसी प्रकार J2=1πR2 (चालक की लंबाई के अनुदिश)
पहले चालक के अंदर विद्युत क्षेत्र है
E2=ρ2lπR2 (चालक की लंबाई के अनुदिश)
चरण II: परिसीमा के पास छोटे बेलनाकार क्षेत्र पर विचार कीजिए और गॉस के नियम को लागू कीजिएः हम परिसीमा पर एक छोटे बेलनाकार क्षेत्र पर विचार करते है।
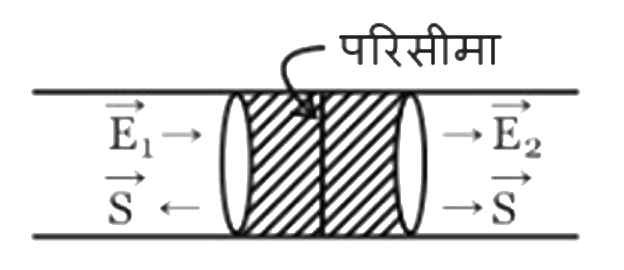
बेलनाकार क्षेत्र का क्षेत्रफल है
S=πR2
इस क्षेत्र से गुजरने वाला कुल फ्लक्स है
ϕ=ϕ1+ϕ2=→E1.→S+→E2→S
=E1Scos1802+E2Scos0∘=−
E1S+E2S=(E2−E1)S
गॉस के नियम के अनुसार
ϕ=qε0
या (E2−E1)=qSε0=σε0
∴ परिसीमा पर पृष्ठ आवेश घनत्व है
σ=(E2−E1)ε0
E1 और E2 के मान रखने पर हम प्राप्त करते हैं
∴σ=(ρ2j−ρ1j) या σ=(ρ2−ρ1)j
∴σ=ε0(ρ2−ρ1)1πR2
या σπR2=ε(ρ2−ρ1)I
या q=ε0(ρ2−ρ1)I
परिसीमा पर आवेश q=ε0(ρ2−ρ1)I
Topper's Solved these Questions
Similar Questions
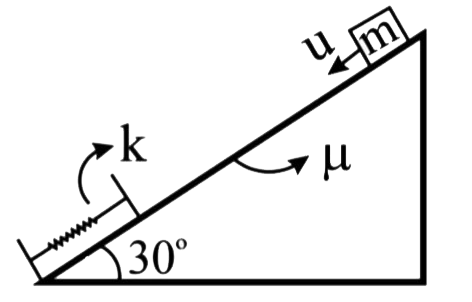
1 kg द्रव्यमान का एक गुटका μ=1√3 के एक खुरदरे आनत तल के शीर्ष से मुक्त किया जाता है। गुटके की प्रारंभिक चाल 2ms−1 है। चित्र के अनुसार नियतांक k=1Nm−1 की एक स्प्रिंग अज्ञात लंबाई के आनत तल के आधार से जुड़ी हुई है। स्प्रिंग का अधिकतम संपीडन ज्ञात कीजिए ।(उत्तर मीटर में दीजिए)।
View Solutionएक चल कुंडली धारामापी में एक प्रतिरोध G है, जब इससे विद्युत धारा Ig प्रवाहित होती है, तब पैमाने पर पूर्ण विक्षेप उत्पन्न होता है। इससे RA प्रतिरोध का शंट जोड़कर इसे 0 से I0(>Ig) परास के ऐमीटर में परिवर्तित किया जा सकता है। यदि इससे श्रेणी में Rv प्रतिरोध को जोड़कर इसे 0 से V=I0G परास के वोल्टमापी में भी परिवर्तित किया जा सकता है, तो निम्न में से कौन सा विकल्प सही है?
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionएक वृत्त का केंद्र (2x−1,3x+1) है। x ज्ञात कीजिए यदि वृत्त (-3,-1) में से गुजरे और व्यास की लम्बाई 20 मात्रक हो।
View Solutionसीधे चालक से विद्युत् धारा प्रवाहित होने के कारण चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही चालक पर चुंबकीय बल |दो समांतर धारावाही चालक के बीच बल-ऐम्पियर
View Solutionविद्युत धारावाही चालक पर चुंबकीय बल |दो समांतर धारावाही चालक के बीच बल-ऐम्पियर
View Solutionसमान रूप से आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता व उस पर आधारित प्रशन
View Solution(-1-1) और (4, 2) से समान दूरी पर स्थित बिन्दुओं के बिन्दुपथ का समीकरण है
View Solutionनिम्नलिखित में से किस स्पीशीज़ के बाह्यतम कोश और साथ ही साथ उपांत्य कोश में इलेक्ट्रॉनों की समान संख्या होती है?
View Solutionअभिक्रिया a+bhArrc+d के लिए प्रार में a और b की सांद्रताएं समान होती है। और साम्यावस्था पर d की सांद्रता a की सांद्रता से दोगुनी होती है। अभिक्रिया के लिए साम्य स्थिरांक क्या होगा?
View SolutionHe+ की परमाणु संरचना, n2 से n1 स्तर में संक्रमण के कारण उत्पन्न होती है। यदि n1+n2=3 है और n2–n1=1 है, तो He+ में इस श्रेणी के लिए संक्रमण का λ(nm में) ज्ञात कीजिए।
View Solutionनिम्नलिखित में से किस प्रजाति में σ और π बंधों की संख्या समान होती है?
View Solutionविभवांतर V_(esu) पर राखी दो आवेशित प्लेटो के मध्य गर्म तंतु से इलेक्ट्रानो की एक धारा प्रवाहित की गई| यदि e और m क्रमश: इलेक्ट्रान के आवेश और द्रव्यमान है, तो h//lamda (जहाँ lamda इलेक्ट्रान तरंग से सम्बंधित तरंगदैर्ध्य है) का मान क्या है ?
View Solutionकिस आरेख के अनुसार, एक सेल के सिरों पर विभवांतर, सेल से प्रवाहित होने वाली विद्युत् धारा के साथ परिवर्तित होता है?
View Solutionनिम्नलिखित यौगिकों में से कौनसा इलेक्ट्रॉनस्नेही के साथ-साथ एक नाभिकस्नेही के समान व्यवहार करता है?
View Solution
