गतियों के संयोजन द्वारा प्राप्त सरल आवर्त गति का विस्थापन समीकरण क्या होगा?
x1=2sinωt,x2
=4sin(ωt+π6) और x3
=6sin(ωt+π3)
A
x=10.25sin(ωt+ϕ)
B
x=10.25sin(ωt−ϕ)
C
x=11.25sin(ωt+ϕ)
D
x=11.25sin(ωt−ϕ)
Text Solution
The correct Answer is:C
परिणामी समीकरण निम्न है
x=Asin(omegt+ϕ)
∑Ax=2+4cos30∘+6cos60∘
=8.46
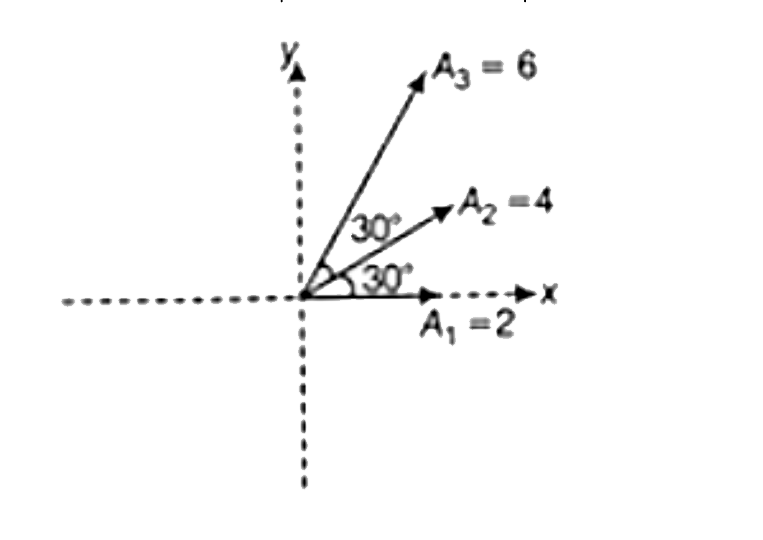
और ∑Ay=4sin30∘+6cos30∘=7.2
∴A=√(∑Ax)2+(∑Ay)2
=√(8.46)2+(7.2)2=11.25
और tanϕ=∑Ay∑Ax=7.28.46=0.85
⇒ϕ=tan−1(0.85)=40.4∘ है।
इस प्रकार, संयुक्त गति का विस्थापन समीकरण निम्न है
x=11.25sin(ωt+ϕ)
जहाँ, =40.4∘
|
Topper's Solved these Questions
Knowledge Check
The motion of a particle is given by x=Asinωt+Bcosωt. The motion of the particle is
Anot simple harmonicBsimple harmonic with amplitude A + BCsimple harmonic with amplitude (A+B)2Dsimple harmonic with amplitude √A2+B2Two sinusoidal waves are superposed. Their equations are
y1=Asin(kx−ωt+π6)andy2=Asin(kx−ωt−π6)
the equation of their resultant isAy2=Asin(kx−ωt−π6) The equation of resultant wave isBy=A√3sin(kx−ωt)Cy=A√3sin(kx−ωt)Dy=A√3sin(kx−ωt−π3)Two waves having equaitons
x1=asin(ωt+ϕ1),x=asin(ω+ϕ2)
If in the resultant wave the frequency and amplitude remain equal to those of superimposing waves. Then phase difference between them isAπ6B2π3Cπ4Dπ3
