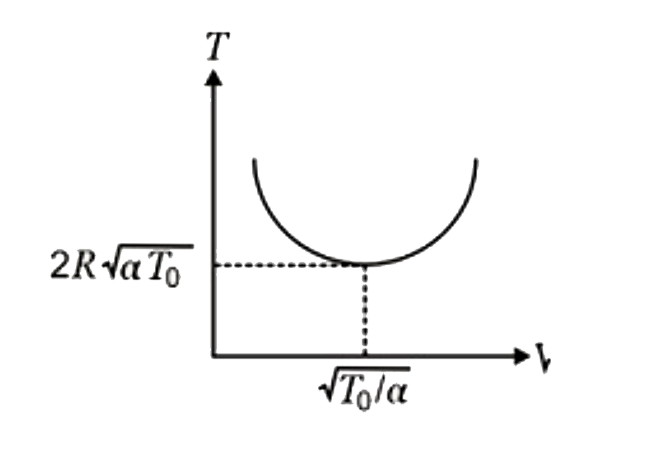
प्रक्रम T=T0+αV2 में एक आदर्श गैस का न्यूनतम प्राप्त करने योग्य दाब ज्ञात कीजिए जहां T0 और α धनात्मक स्थिरांक है और V गैसा क ेएक मोल का आयतन है।
2R√αT0
3R√αT0
3R
3R√αT02
The correct Answer is:A
दिया गया है
T=T0+αV2....i
गैस के 1 मोल के लिए PV=RT
तब V=RTP
इस मान को समीकरण i में प्रतिस्थापित करने पर हम प्राप्त करते है।
T=T0+alϕa(RTP)2=T0+αR2T2P2
या TP2=T0P2+αR2T2
या P=√αRT(T−T0)−1/2.ii
अवकल करने के बाद हम प्राप्त करते हैं।
dPdT
=√αR
=√αR
[(T−T0)−1/2−12T(T−T0)3/2]
न्यूनतम दाब के लिए
dPdT=0
∴0=√α
R[(T−T0)−1/2−12T(T−T0)3/2]
हल करने केबाद T=2T0
Pmin=√αR2T0(2T0−T0)−1/2
=2R√αT0
Topper's Solved these Questions
Similar Questions
यदि हाइड्रोजन परमाणु की लाइमैन श्रेणी की श्रेणी सीमा तरंगदैर्ध्य 912 Å है, तब हाइड्रोजन परमाणु की बामर श्रेणी की श्रेणी सीमा तरंगदैर्ध्य है:
View Solutionएक समतल धरातल पर बिना ढाल वाला गोलीय राजमार्ग वक्र 90∘ का कोण बनाता है। राजमार्ग पर 108kmh−1 की चाल से यातायात चलता है, और किसी वाहन पर अभिकेंद्र बल उसके भार के 110 से अधिक नहीं हो पाता है। वक्र की न्यूनतम लंबाई (km में) लगभग क्या है?
View Solutionएक चतुष्फलक के चारो शीर्ष O(0,0,0), A(1,2,1),B(2,1,3) और C(-1,1,2) है चतुफलक का आयतन ज्ञात कीजिए।
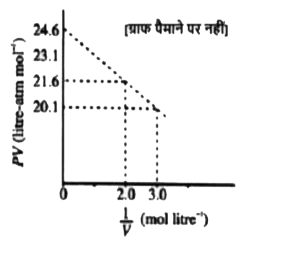
View Solutionएक मोल वांडर वाल गैस के लिए b=0 और T=300K पर, PV और 1V का आलेख नीचे दिखाया गया है। वांडर वाल स्थिरांक a (atmlitre2mol−2)0 का मान है:
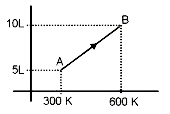
View Solutionचित्र में दर्शाये अनुसार एक आदर्श गैस के एक मोल को A→B अनुसार लिया गया है। प्रक्रम में निहित कार्य का परिमाण है: (R=253JmolK)
View Solution24°C पर एक शर्करा विलयन का परासरण दाब 2.5 वायुमंडल है। मोल/लीटर में विलयन की सांद्रता ज्ञात कीजिए:
View Solution1 atm के बाह्य दाब के अंतर्गत गतिशील पिस्टन वाले एक निर्वातित पात्र में, He के 0.1 मोल और एक अज्ञात यौगिक के 1.0 मोल (0°C पर 0.68 atm वाष्प दाब) को रखा जाता है। आदर्श गैस व्यवहार मानते हुए, 0°C पर साम्यावस्था पर गैस का कुल आयतन (L में) लगभग x L के समान है। x के मान की गणना कीजिए।
View Solutionवाष्पशील घटक A और B के मिश्रण का कुल वाष्प दाब (टॉर में) P=254 -119 X_(A) है। जहां मिश्रण में, A का मोल प्रभाज X_(A) है। इसलिए, P_(A)^(0) और P_(B)^(0) (टॉर में) हैं:
View Solutionएक आदर्श गैस का विसरण गुणांक इसके माध्य मुक्त पथ और माध्य चाल के समानुपाती होता है। एक आदर्श गैस का परम ताप 4 गुना बढ़ाया जाता है और इसका दाब 2 गुना बढ़ाया जाता है। परिणामस्वरूप, इस गैस का विसरण गुणांक x गुना बढ़ जाता है। x का मान है:
View Solutionएक एकपरमाण्विक वास्तविक गैस का एक मोल समीकरण p (V — b) = RT को संतुष्ट करता है जहाँ b एक स्थिरांक है। गैस के लिए अंतरापरमाणुक विभव V(r) और अंतरापरमाणुक दूरी r का संबंध निम्नानुसार दर्शाया जाता है
View Solutionनिम्नलिखित में से कोनसा आयतन (V ) और तापमान ( T ) ग्राफ एक वायुमंडलीय दाब पर एक आदर्श गैस के एक मोल के व्यवहार को दर्शाता है
View Solution1 atm के बाह्य दाब पर He के 0.1 मोल और अज्ञात यौगिक ( 0^(@)C पर वाष्प दाब 0.68 atm है। )के 1.0 मोल को गतिशील पिस्टन वाले एक निर्वातित पात्र में लिया गया है। आदर्श गैस के व्यवहार पर विचार करते हुए 0^(@)C पर गैसों का कुल आयतन (लीटर में) लगभग है
View Solutionजब गैस को जल के माध्यम से 298K पर बुदबुदाया जाता है, तब गैस का एक तनु विलयन प्राप्त होता है। गैस के लिए हेनरी स्थिरांक 100 Kbar है। यदि गैस 1 बार का दाब डालती है, तो 1 लीटर जल में विलीन गैस के मोलो की संख्या x×10−5 है। यहाँ x का मान ज्ञात कीजिए?
View Solutionनिम्नलिखित अभिक्रिया के अनुसार गैसीय बेन्जीन। एक निकैल उत्प्रेरक की उपस्थिति में हाइड्रोजन गैस के साथ अभिक्रिया करता है और गैसीय साइक्लोहेक्सेन का उत्पादन करता है। C_6H_(6 (g)) + 3H_(2 (g)) to C_6H_(12 (g)) एक अज्ञात आयतन में CH_6 और आधिक्य में H_2 के एक मिश्रण का दाब 60 mm Hg है। गैस, निकैल उत्प्रेरक से पारित हो जाने और संपूर्ण बेन्जीन, साइक्लोहेक्सेन में परिवर्तित हो जाने के बाद, समान आयतन और ताप पर गैस का दाब 30 mm Hg था। प्रारंभिक आयतन में मौजूद C_6H_6 (आयतन अनुसार) का प्रभाज 1/y है। 'y' का मान है
View Solutionएक आदर्श गैस के दस मोलों को एक बंद पात्र में भरा जाता है । पात्र में बेलन और पिस्टन के प्रकार की व्यवस्था है और 0.821 atm पर गैस का दाब स्थिर रहता है। निम्नलिखित में से कौन सा आलेख logV और logT के परिवर्तन का सही निरूपण करता है? (V= आयतन(लीटर में) और T= ताप (केलिवन में)
View Solutionआदर्श गैस के 1 मोल का आदर्श गैस समीकरण PV = nRT है। स्थिर आयतन पर P और T के बीच का वक्र, अर्थात समआयतनिक वक्र, निम्न प्रकार आरेखित है, निम्नलिखित में से आयतन का कौन सा क्रम सही है?
View Solution
