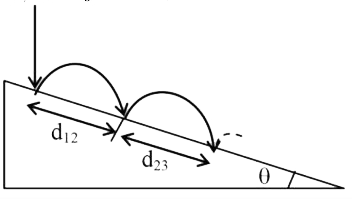
एक प्रत्यास्थ गेंद को एक लंबे आन तल पर गिराया जाता है यदि उछलता है तोवह तल से पुनः टकराता है उछलता है और इसी तरह आगे भी। हम पहली और दूसरी टक्कर के बिंदु के बीच की दूरी को d12 और दूसरे और तीसरे टक्कर के बिंदु के बीच की दूरी को d23 मानते हैं तो d12/d23 का अनुपात ज्ञात कीजिए।
21
12
41
14
The correct Answer is:B
यदि हम निर्देशांक निकाय को घुमाते हैं ताकि रैंप क्षैतिज हो तब मुक्त पतन वेग में दो घटक होंगे एक नीचे की ओर ay=−gcosθ और एक क्षैतिज ax=gsinθ है। इस फ्रेम में प्रारंभिक वेग के दिए गए घटक निर्मित है
Vy=V0cosθ और Vx=V0sinθ
प्रत्येक उछाल के लिए समय है
tb=2Vy−ay=2V0g
क्षैतिज विस्थापन Δx=Vxt+0.5axt2
दिए गए समीकरण
d12=V0sinθ(2V02)
+0.5sinθ(2V0g)2
=4V20sinθg
d13=V0sinθ(4V0g)
+0.5gsinθ(4V0g)2
=12V20sinθg
चूंकि d23=d13−d12=8V20−sinθg
d12d23=12
Topper's Solved these Questions
Similar Questions
100 W का एक सोडियम लैंप सभी दिशाओं में एकसमान रूप से ऊर्जा करता है। सोडियम प्रकाश की तरंगदैर्ध्य 589nm है। सोडियम प्रकाश के साथ संबद्ध प्रति फोटॉन ऊर्जा (eV में ) है:
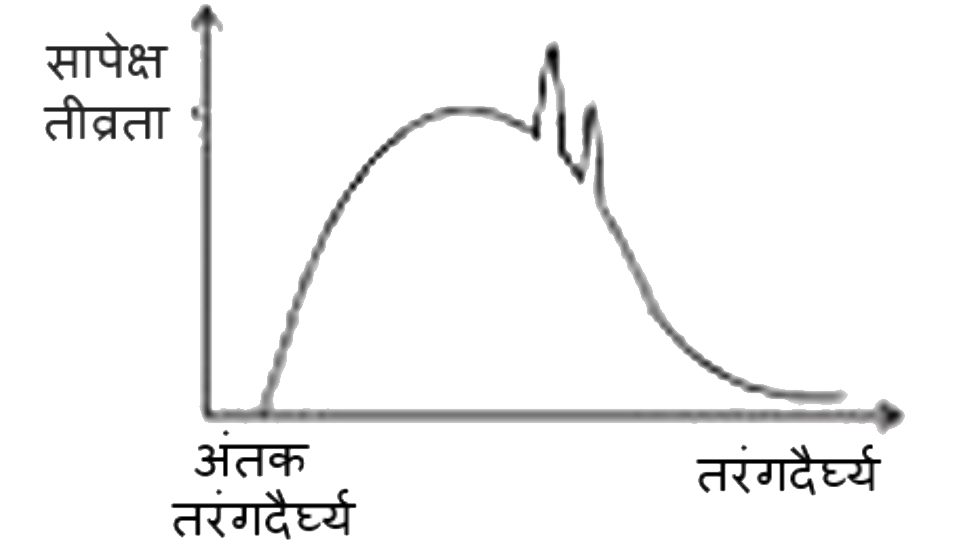
View Solutionतांबे के लक्ष्य से, इलेक्ट्रॉनों की एक किरणपुंज के टकराने पर X - किरणें उत्पादित होती है। इसका स्पेक्ट्रम निम्नानुसार दिखाया गया है। वोल्टता को समान रखते हुए यदि तांबे के लक्ष्य को एक दूसरी धातु से प्रतिस्थापित किया जाता है, तो अंतक तरंगदैर्ध्य और नए स्पेक्ट्रम की अभिलाक्षणिक रेखाएँ पुराने की तुलना में किस प्रकार परिवर्तित होंगी
View Solutionएक सरल रेखा द्वारा अक्षो के बीच काटे गये अन्तः खण्ड को बिंदु (7,9),3:1 के अनुपात में अन्तः विभाजित करता है रेखा का समीकरण ज्ञात कीजिए
View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
View Solutionदो बिंदुओं P और Q के स्थिति सदिश क्रमशः 2¯a+¯b और ¯a−2¯b है। एक बिंदु R का स्थिति सदिश ज्ञात कीजिए जो रेखा खण्ड PQ को 1:2 के अनुपात में अंतः तथा बाहृातः विभाजित करता है।
View SolutionA और B दो बिंदु है। बिंदुओं A और B के स्थिति क्रमशः 6¯a−2¯b और ¯b−9¯a है। वह अनुपात ज्ञात कीजिए जिसमें बिंदु P जिसका स्थिति सदिश ¯a−¯b है रेखाखण्ड AB को विभाजित करता है।
View Solutionरेखा - युग्म के बीच का कोण ज्ञात कीजिए --- बिंदु (3, 1, 4) और (7, 2, 12) को मिलाने वाली रेखा।
View Solutionबिंदुओं (3,1) और (0,y) के बीच की दूरी 5 है। y ज्ञात कीजिए।
View Solutionयदि एक कण पर क्रिया करते हुए तीन बल संतुलन में हैं। पहले दो के बीच का कोण 90∘, ... दूसरे और तीसरे के बीच का कोण 120∘ हैं, तो बलों का अनुपात ज्ञात कीजिए।
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View SolutionA certain sum is divided between A, B, C and D such that the ratio of the shares of A and B is 1 : 3, that of B and C is 2 : 5 and that of C and D is 2 : 3. If the difference between the shares of A and C is ₹3,510, then the share of D is :
एक राशि A, B, C और D के बीच विभाजित की जाती है, जैसे A और B के शेयरों का अनुपात 1: 3 है, B और C का अनुपात 2: 5 है और C और D का अनुपात 2 :3 है. यदि A और C के शेयरों के बीच अंतर ₹3,510 है, तो D का हिस्सा है
View SolutionTwo circles of radii 7 cm and 9 cm intersect at the points A and B. If AB = 10 cm and the distance between the centres of the circle is x cm, then the value of x is :
त्रिज्या 7 सेमी और 9 सेमी वाले दो वृत्त एक दूसरे को बिंदु A और बिंदु B पर काटते हैं | यदि AB =10 सेमी है और वृत्तों के केंद्रों के बीच की दूरी x सेमी है, तो x का मान क्या होगा ?
View SolutionFrom the top of a hill 240m high the angle of depression of the top and of the bottom of a pole are 30^@ and 60^@ , respectively. The difference (in m) between the height of the pole and its distance from the hill is : एक पहाड़ी के शीर्ष जो 240 मीटर ऊँचा है| से एक खम्भे के ऊपर और निचे के तल पर कोण क्रमश 30^@ और 60^@ है। खम्भे की ऊँचाई और पहाड़ी से उसकी दूरी के बीच का अंतर (m) है
View SolutionTwo circles of radii 7 cm and 9 cm intersect at the points A and B. If AB=6cm, and the distance between the centres of the circles is x cm, then the value of x (to the closest integer) is: 7 cm और 9 cm त्रिज्या के दो वृत्त, बिंदु A और B पर एक दूसरे को काटते हैं| अगर AB=6 cm है, और वृत्त के केंद्रों के बीच की दूरी x cm है तो x का मान (निकटतमें पूर्णाक में) है:
View Solutionपदार्थ A और B के बीच अभिक्रिया को निम्न प्रकार दर्शाया गया है
A+B−→C इस अभिक्रिया की दर से निम्न प्रेक्षणों को प्राप्त किया जाता है

View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solution
