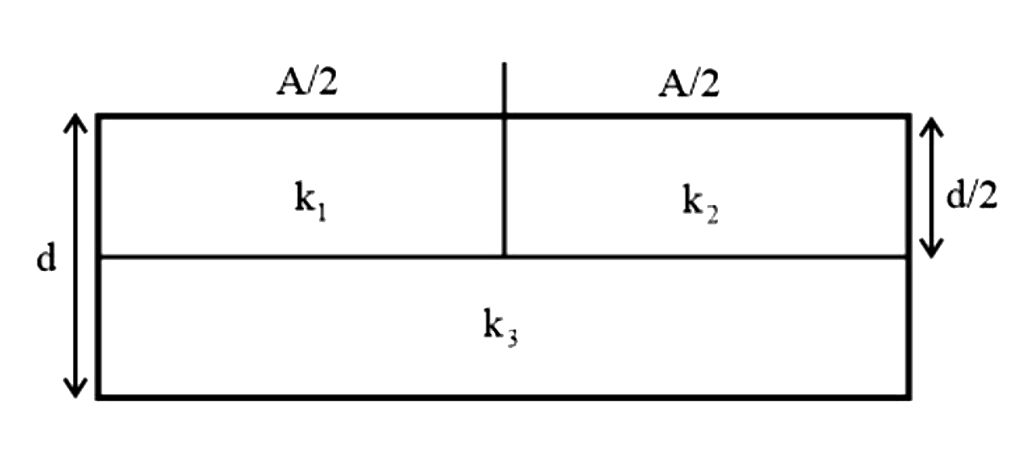
क्षेत्रफल A, प्लेट पृथक्करण d और धारिता C के एक समांतर पट्टिका संधारित्र को परावैद्युतांक k1,k2 और k3 के तीन परावैद्युत पदार्थ से भरा जाता है, जैसा कि दिखाया गया है। यदि संधारित्र में समान धारिता C प्राप्त होने के लिए एकल परावैद्युत पदार्थ का उपयोग किया जाना है, तो इसका परावैद्युतांक k निम्न द्वारा दिया जाता है :
k=k1+k2+2k3
k=k1k2k1+k2+2k3
1k=1k1+1k2+12k2
1k=1k1+k2+12k3
The correct Answer is:D
धारिताएँ, C1=k1ε0A/2[d/2]=k1ε0Ad
C2=k2ε0A/2d/2=k0ε0Ad
or C3=k3ε0A/2d/2=2k3ε0Ad
समतुल्य धारिता निम्न द्वारा दी जाती है:
⇒1Cतुल्य=1C1+C2+1C2=1ε0Ad(k1+k2)+1ε0Ad×2k3
⇒Cतुल्य=[1k1+k2+1(2k3]−1.εAd]
⇒1k=[1k1+k2+12k3](∴C=kεAd)
k=k1k3k1+k3+k2k3k2+k3
Cतुल्य=ε0A/2d2k1+d2k3+ε0A/2d2k2+d2k3
=ε0Ad(k1.k3+k1+k3+k2.k3k2+k3)
∴ समतुल्य
k=k1k2k1+k2+k2k3k2+k3
Topper's Solved these Questions
Similar Questions
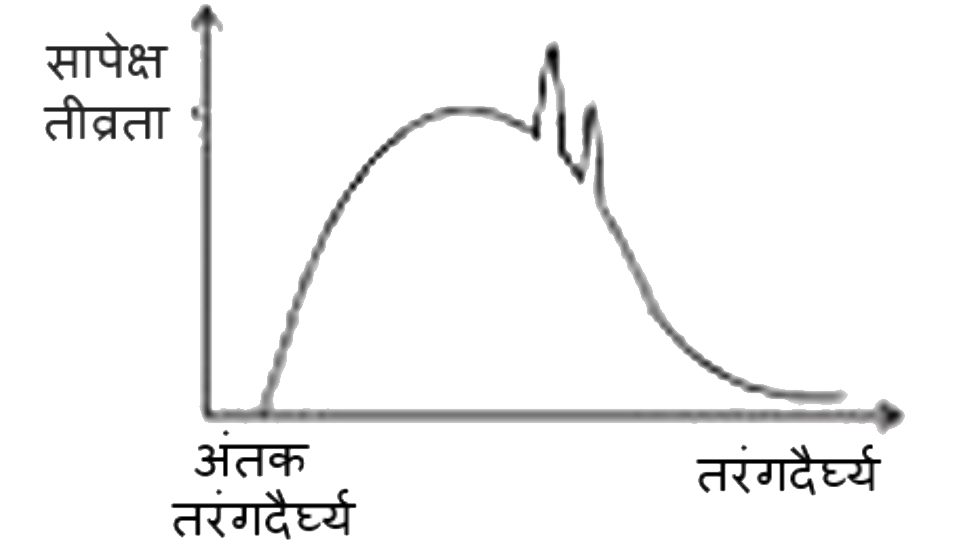
तांबे के लक्ष्य से, इलेक्ट्रॉनों की एक किरणपुंज के टकराने पर X - किरणें उत्पादित होती है। इसका स्पेक्ट्रम निम्नानुसार दिखाया गया है। वोल्टता को समान रखते हुए यदि तांबे के लक्ष्य को एक दूसरी धातु से प्रतिस्थापित किया जाता है, तो अंतक तरंगदैर्ध्य और नए स्पेक्ट्रम की अभिलाक्षणिक रेखाएँ पुराने की तुलना में किस प्रकार परिवर्तित होंगी
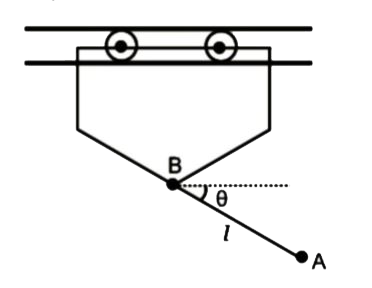
View Solutionद्रव्यमान mA और लंबाई ।l का सरल लोलक A द्रव्यमान mB की ट्रॉली B से निलंबित है। यदि निकाय को θ=0 पर विराम से मुक्त किया जाता है, तो ट्रॉली का वेग vB ज्ञात कीजिए। घर्षण नगण्य है
View Solutionसंधारित्र की धारिता पर परावैद्युत का प्रभाव | समान्तर-प्लेट संधारित्र की धारिता जब उसकी प्लेटों के बीच आंशिक रूप से परावैद्युत पदार्थ रखा हो
View SolutionRecap|परावैद्युतांक पदार्थ |एकसमान विधयुत क्षेत्र मे चालक तथा परावैद्युत पदार्थ |परावैद्यु माध्यम तथा परावैद्युतांक |परावैद्युत के प्रकार |OMR|Summary
View SolutionRecap|समांतर प्लेट संधारित्र की धारिता जब प्लेटों के बीच परावैद्युत माध्यम भरा हो |OMR|Summary
View Solutionसंधारित्र और परावैद्युत भरा हुआ संधारित्र में उष्मा का क्षय
View Solutionपरावैद्युत संधारित्र और परावैद्युत भरा हुआ संधारित्र व परावैद्युत नहीं भरा हुआ संधारित्र में उष्मा का क्षय
View Solutionसंधारित्रो का संयोजन - प्रश्न |परावैद्युतांक का प्रभाव |समांतर प्लेट संधारित्र के अंदर परावैद्युत पट्टिका |OMR|Summary
View Solutionपदार्थ A और B के बीच अभिक्रिया को निम्न प्रकार दर्शाया गया है
A+B−→C इस अभिक्रिया की दर से निम्न प्रेक्षणों को प्राप्त किया जाता है

View Solutionजब एक अवाष्पशील पदार्थ के 10.6g को ईथर के 750 g में विलेय किया जाता है, तो इसका क्वथनांक 0.266∘C बढ़ जाता है । पदार्थ का अणु भार है: (दिया गया है: ईथर के लिए मोलल क्वथनांक स्थिरांक 2.0∘C kg/mol है) निकटतम पूर्णांक में अपना उत्तर दीजिये
View Solutionजब logk और 1/T के बीच एक आलेख आलेखित किया जाता है, तो हमें एक आलेख प्राप्त होता है, जैसा कि नीचे दर्शाया गया है आलेख में ढाल का मान क्या है?
View Solutionएक यौगिक (A) का उपयोग सॉल्वे प्रक्रम में अमोनिया की पुनः प्राप्ति के लिए धावन सोडा के विचरन में किया जाता है। जब CO_(2) को (A) के जलीय विखंडन में बुदबुदाया जाता है तो विलयन दूधिया हो जाता है। इसका उपयोग विसंक्रामक प्रकृति के कारण सफेदी में किया जाता है। A का रासायनिक सूत्र क्या होगा?
View SolutionNaCl के संकुलन प्रभाज के लिए निम्नलिखित में से कौन सा व्यंजक सही है, यदि एक फलक और एक विकर्ण से a- आयन को हटा दिया जाता है?
View Solutionबोश प्रक्रम का उपयोग हाइड्रोजन गैस के उत्पादन के लिए किया जाता है, दी गई गैस में से किस गैस का उपयोग इसके लिए किया जाता है
View Solutionफॉर्मेल्डिहाइड और एसीटैल्डिहाइड के मध्य विभेद करने के लिए किस अभिकर्मक का उपयोग किया जाता है?
View Solutionकैल्सियम के निर्माण के लिए निम्नलिखित में से किस प्रक्रम का उपयोग किया जाता है?
View Solution
