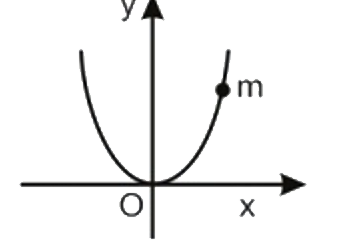
द्रव्यमान m का एक मनका परवलयिक तार पर स्थित है, जिसका अक्ष ऊर्ध्वाधर है और शीर्ष मूल बिंदु पर है, जैसा कि चित्र में दिखाया गया है और जिसका समीकरण x2=4ay है। तार का फ्रेम स्थिर किया जाता और मनका इस पर बिना घर्षण के फिसल सकता है। मनके को तार के फ्रेम पर बिंदु y = 4a से विरामावस्था से छोड़ा जाता है। जब मनका y = a द्वारा दी गई स्थिति तक पहुँचता है, तब इसका स्पर्शरेखीय त्वरण है:
g2
√3g2
g√2
g√5
The correct Answer is:C
x2=4ay
y के सापेक्ष अवकलन करने पर, हमें निम्न प्राप्त होता है
dydx=x2a
इसे एक आनत तल के रूप में माना जा सकता है
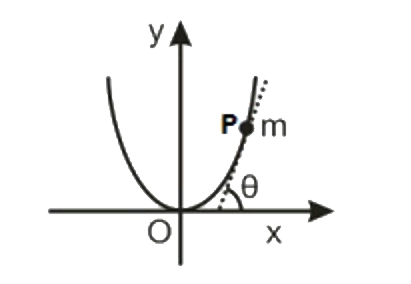
∴(2a,a) पर dydx=1
⇒ अत: θ=45∘
स्पर्शरेखीय दिशा के अनुदिश भार का घटक mg sin θ है।
इसलिए स्पर्शरेखीय त्वरण निम्न है
gsinθ=g√2
Topper's Solved these Questions
- JEE MAIN TEST - 88 BOOK - NTA MOCK TESTSCHAPTER - JEE MAIN TEST - 88 EXERCISE - भौतिक विज्ञान(विषयपरक आंकिक)
5 Videos
- JEE MAIN TEST - 47 BOOK - NTA MOCK TESTSCHAPTER - JEE MAIN TEST - 47 EXERCISE - भौतिक विज्ञान
25 Videos
- JEE MAIN TEST -55BOOK - NTA MOCK TESTSCHAPTER - JEE MAIN TEST -55EXERCISE - भौतिक विज्ञान
25 Videos
Similar Questions
एक लोलक के गोलक का द्रव्यमान m = 2 kg है और डोरी की लंबाई l है। इसे ऊर्ध्वाधर से 90∘ से विस्थापित किया जाता है और छोड़ दिया जाता है। डोरी कितना न्यूनतम तनाव (N में) सहन करने में सक्षम होगी ताकि गति के दौरान टूटे नहीं?
View Solutionएक गेंद को एक चिकने आनत तल पर गिराया जाता है और यह प्रेक्षित किया जाता है कि यह संघट्ट के बाद क्षैतिज रूप से गति करती है। तल और गेंद के बीच प्रत्यावस्थान गुणांक e है। आनत तल का झुकाव कोण है:
View Solutionपानी की सतह की तरंगों (केशिका तरंगों) की चाल की पानी के घनत्व (ρ), उनकी तरंग दैर्ध्य (λ) और पृष्ठ तनाव (γ) पर निर्भरता है -
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionसमीकरण x + y =7 का आलेख x-अक्ष को किस बिंदु पर काटता है ?
View Solutionएक बिंदु P, x-अक्ष पर और एक अन्य बिंदु Q, y-अक्ष पर स्थित है। (i) बिंदु P की कोटि ज्ञात कीजिए।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जो बिंदुओं ( 1,0,0), ( 0,1,0) तथा ( 0,0,1) से होकर जाता है तथा जिसका केंद्र समतल 3x−y+z=2पर स्थित है।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जो बिंदुओं (1,0,0) , ( 0,1,0) तथा ( 0,0,1) से होकर जाता है तथा जिसका केंद्रे समतल x - y + z = 2 पर स्थित है।
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View Solution(-1-1) और (4, 2) से समान दूरी पर स्थित बिन्दुओं के बिन्दुपथ का समीकरण है
View Solution5 बार और 300K पर एक आदर्श एक्परमाणविक गैस के दो मोल के 1 बार के ब्रह्म डाब तक अनुत्क्रमणीय रूप से प्रसारित किया जाता है गैस दवरा किया गया कार्य xR (बार लीटर में ) है x का मान है
View Solution
