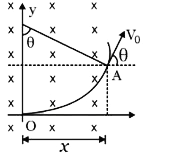
प्रति इकाई द्रव्यमान आवेश के एक कण चुंबकीय क्षेत्र और के लिए चुंबकीय क्षेत्र में वेग से मूल बिंदु से मुक्त किया जाता है। समय पर कण का :-निर्देशांक होगा:
The correct Answer is:C
Topper's Solved these Questions
Similar Questions
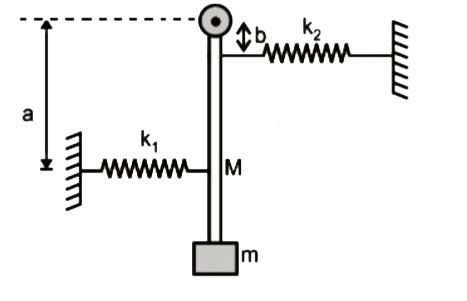
द्रव्यमान M और लंबाई L की एक छड़ के एक सिरे पर कब्ज़ा लगा होता है और इसके निचले सिरे पर द्रव्यमान m का एक गुटका होता है। बल नियतांक k1 का एक स्प्रिंग कब्जे से a दूरी पर स्थापित किया जाता है और बल नियतांक k2 का एक दूसरा स्प्रिंग कब्जे से b दूरी पर स्थापित किया जाता है, जैसाकि चित्र में दर्शाया गया है।यदि पूरी व्यवस्था एक चिकनी क्षैतिज मेज के ऊपर टिकी हुई है, तब कंपन की आवृत्ति ज्ञात कीजिए।
View Solutionएक तत्व के 12 g के गुटके को एक कोष्ठ में रखा जाता है। यह तत्व 15 वर्ष की अर्द्ध-आयु का एक रेडियोधर्मी तत्व है। कितने वर्षों के बाद कोष्ठ में तत्व का केवल 1.5 g होगा?
View SolutionThe position of a particle at time t is given by the relation x(t) = ( v_(0) /( alpha)) ( 1 - c^(-at)) , where v_(0) is a constant and alpha gt 0 . Find the dimensions of v_(0) and alpha .
View SolutionA particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would be
View SolutionAn electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=B0ˆj. Then it's de-Broglie wavelength
View SolutionThe position of a particle at time t is given by the relation x(t)=(v0α)(1−e−αt) where v0 is a constant and α>0. Find the dimensions of v0 and α
View SolutionIn the region between the plane z=0 and z=a (a gt 0) , the uniform electric and magnetic fields are given by vecE=E_(0)(hatk-hatj) , vecB=B_(0)hati . The region defined by a le z le b contains only magnetic field vecB= -B_(0)hati . Beyond z gt b no field exits. A positive point charge q is projected from the origin with velocity v_(0)hatk . Assuming the mass of the particle to be (2)/(3)(qE_(0)a)/(v_(0)^(2)) . The value of E_(0) such that the particle moves undeviated upto the plane z=a is
View SolutionIn the region between the plane z=0 and z=a(a>0), the uniform electric and magnetic fields are given by →E=E0(ˆk−ˆj), →B=B0ˆi. The region defined by a≤z≤b contains only magnetic field →B=−B0ˆi. Beyond z>b no field exits. A positive point charge q is projected from the origin with velocity v0ˆk. Assuming the mass of the particle to be 23qE0av20.
When the particle just reverse its direction, all the fields are switched off. Time taken by the particle to touch the plane z=0 from that instant is
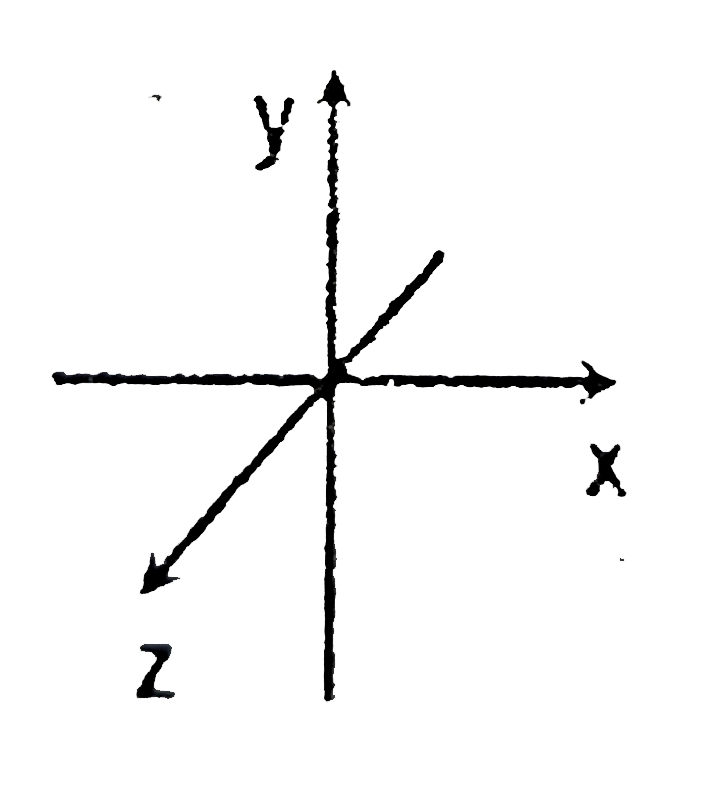
View SolutionThe position of a particle at time t, is given by the equation, x(t) = (v_(0))/(alpha)(1-e^(-alpha t)) , where v_(0) is a constant and alpha gt 0 . The dimensions of v_(0) & alpha are respectively.
View SolutionA charged particle of specific charge (Charge/mass) alpha is released from origin at time t=0 with a velocity given as vecv=v_(0)(hati+hatj) The magnetic field in region is uniform with magnetic induction vecB=B_(0)hati . Coordinates of the particle at time t=(pi)/(B_(0)alpha) are:
View SolutionA particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would be
View SolutionAn electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=B0ˆj
Then it's de-Broglie wavelength
View SolutionAn electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=B0ˆj. Then it's de-Broglie wavelength
View SolutionAn electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=B0ˆj. Then it's de-Broglie wavelength
View SolutionChoose the correct option: A particle of charge per unit mass alpha is released from origin with a velocity vecv=v_(0)hati in a magnetic field vec(B)=-B_(0)hatk for xle(sqrt(3))/2 (v_(0))/(B_(0)alpha) and vec(B)=0 for xgt(sqrt(3))/2 (v_(0))/(B_(0)alpha) The x -coordinate of the particle at time t((pi)/(3B_(0)alpha)) would be
View SolutionThe position of a particle at time t is given by the relation x(t)=(v0α)(1−c−at), where v0 is a constant and α>0. Find the dimensions of v0andα.
View Solution