प्रत्येक द्रव्यमान 0.1 kg की दो समरूप गेंदें A और B दो समरूप द्रव्यमान रहित स्‍प्रिंगों से जुड़ी है। जैसा कि चित्र में दिखाया गया है स्‍प्रिंग द्रव्यमान निकाय एक वृत्त के रूप में मुड़ी हुई दृढ़ चिकनी नली के अंदर गति करने के लिए प्रतिबंधित है। नली एक क्षैतिज तल में स्थिर है । गेंदों के केंद्र त्रिज्या 0.06 m के एक वृत्त में गति कर सकते हैं। प्रत्येक स्‍प्रिंग की प्राकृततक लंबाई $0.06 π m$ और स्‍प्रिंग नियतांक $0.1 N m^{- 1}$ है शुरू में दोनों गेंदों को वृत्त के व्यास PQ के सापेक्ष $θ = \frac{π}{6}$ rad कोण से विस्थापित किया जाता है (जैसा कि चित्र में दिखाया गया है) और विराम से छोड़ा जाता है। गेंदों के दोलन की आवृत्‍ति है:

A

$\frac{1}{2 π} H z$

B

$\frac{1}{3 π} H z$

C

$\frac{1}{π} H z$

D

$\frac{1}{4 π} H z$

Text Solution

Verified by Experts

The correct Answer is:C

दिया गया है प्रत्येक गुटके A और B का द्रव्यमान m=0.1kg
वृत्त की त्रिज्या R=0.06m

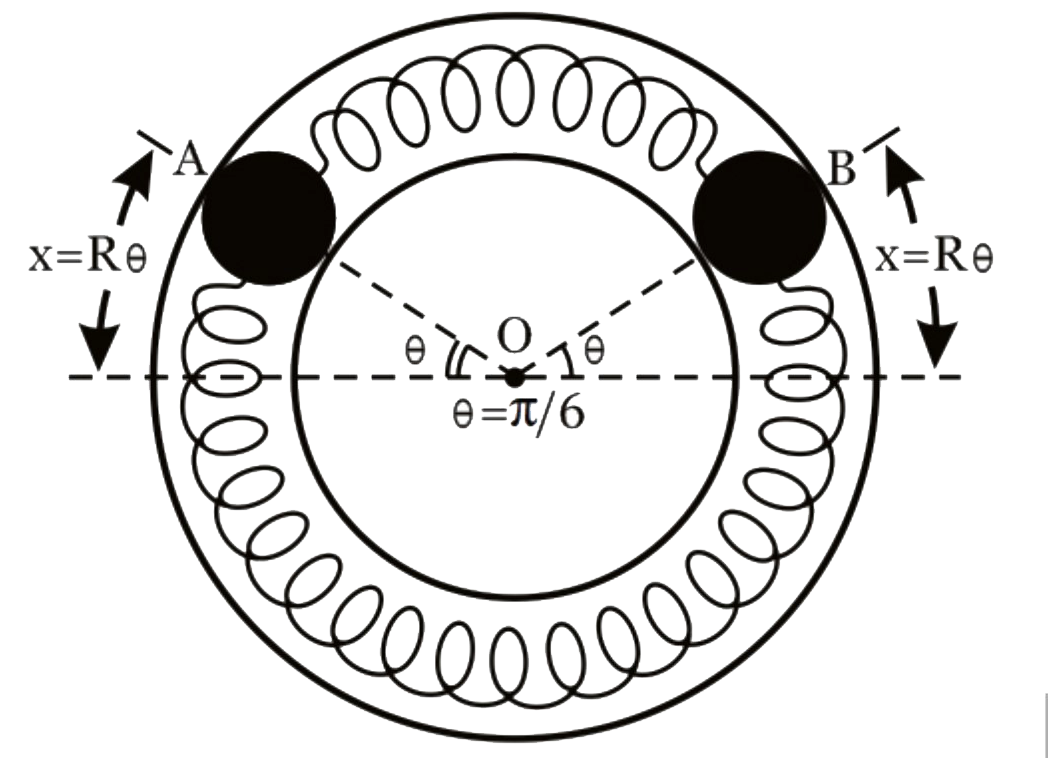
स्‍प्रिंग की प्राकृतिक लंबाई $l_{0} = 0.06 π - π r$ (अर्ध वृत्त) और स्‍प्रिंग नियतांक $k = 0.1 N m^{- 1}$
तानित स्थिति में प्रत्येक सिप्रंग में दीर्घीकरण $x = R θ$
आइए हम A का बल निर्देशक आरेख बनाएं

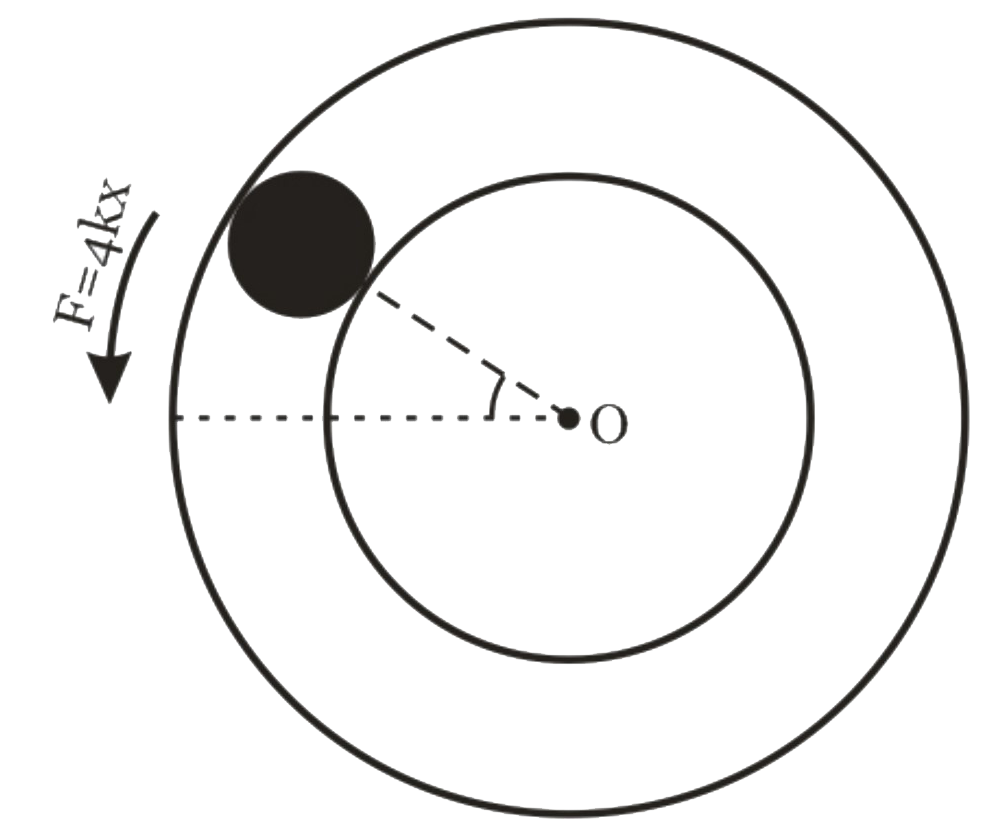
नीचे की ओर स्‍प्रिंग 2x से तानित है और ऊपर की ओर 2x से संपीडित है। इसलिए चित्र में दिखाए गए अनुसार दिशा में एक द्रव्यमान बल $F = 4 k x, A$ पर कार्य करेगा।
मूल बिंदु के परितः इसे बल का प्रत्यानयन आघूर्ण
$τ = - F . R = - (4 k x) R = - (4 k R θ) R$
या $τ = - 4 k R^{2} . θ$ ............i
चूंकि $τ \propto - θ$ प्रत्येक गेंद मूल बिंदु O के परितः कोणीय सरल आवर्त गति करती है।
समीकरण (i) को निम्न रूप में लिखा जा सकता है।
$I α = - 4 k R^{2} θ$
या $(m R^{2}) α = - 4 k R^{2} θ$
या $α = - (\frac{4 k}{m}) θ$
दोलन की आवृत्‍ति $f = \frac{1}{2 π} \sqrt{∣ ∣ ∣ \frac{त्वरण}{विस्थापन} ∣ ∣ ∣} = \sqrt{∣ ∣ ∣ \frac{α}{θ} ∣ ∣ ∣}$
$f = \frac{1}{2 π} \sqrt{\frac{4 k}{m}}$
मानों को प्रतिस्थापित करने पर हमारे पास है
$f = \frac{1}{2 π} \sqrt{\frac{4 \times 0.1}{0.1}} = \frac{1}{π} H z$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

NTA MOCK TESTS-JEE MAIN TEST 100-भौतिक विज्ञान

Home
Ask Doubt
Profile