50 trees are standing in a line such that distance between any two consecutive trees is same. A car takes 18 seconds to travel from 13th tree to 34th tree. How much time (in seconds) will it take to reach from 1st tree to 50th tree?
42
42.85
45
49
The correct Answer is:A
To solve the problem step by step, we need to determine the time it takes for the car to travel from the 1st tree to the 50th tree based on the information given about the travel time between the 13th and 34th trees.
Step 1: Identify the number of trees and distances
We know that there are 50 trees standing in a line, and the distance between any two consecutive trees is the same.
Step 2: Calculate the number of trees between the 13th and 34th trees
To find the number of trees between the 13th and 34th trees, we can calculate:
- The number of trees from the 13th to the 34th tree is given by:
34−13=21 trees
However, since we are counting the trees, we should consider the distance traveled which is between the 13th tree and the 34th tree, meaning there are 21 gaps between them.
Step 3: Calculate the time taken per gap
The car takes 18 seconds to travel from the 13th tree to the 34th tree, which covers 21 gaps. Therefore, the time taken for each gap is:
Time per gap=18 seconds21 gaps=67 seconds per gap
Step 4: Calculate the total number of gaps from the 1st tree to the 50th tree
To find the total number of gaps from the 1st tree to the 50th tree, we calculate:
- The number of gaps between the 1st and 50th trees is:
50−1=49 gaps
Step 5: Calculate the total time to travel from the 1st tree to the 50th tree
Now, we can find the total time taken to travel from the 1st tree to the 50th tree by multiplying the number of gaps by the time taken per gap:
Total time=49 gaps×67 seconds per gap=2947=42 seconds
Conclusion
Thus, the time taken for the car to travel from the 1st tree to the 50th tree is 42 seconds.
---
We know that there are 50 trees standing in a line, and the distance between any two consecutive trees is the same.
To find the number of trees between the 13th and 34th trees, we can calculate:
- The number of trees from the 13th to the 34th tree is given by:
34−13=21 trees
However, since we are counting the trees, we should consider the distance traveled which is between the 13th tree and the 34th tree, meaning there are 21 gaps between them.
The car takes 18 seconds to travel from the 13th tree to the 34th tree, which covers 21 gaps. Therefore, the time taken for each gap is:
Time per gap=18 seconds21 gaps=67 seconds per gap
To find the total number of gaps from the 1st tree to the 50th tree, we calculate:
- The number of gaps between the 1st and 50th trees is:
50−1=49 gaps
Now, we can find the total time taken to travel from the 1st tree to the 50th tree by multiplying the number of gaps by the time taken per gap:
Total time=49 gaps×67 seconds per gap=2947=42 seconds
Thus, the time taken for the car to travel from the 1st tree to the 50th tree is 42 seconds.
Similar Questions
Knowledge Check
50 trees are standing in a line such that distance between any two consecutive trees is same. A car takes 18 seconds to travel from 13th tree to 34th tree. How much time (in seconds) will it take to reach from the first tree to the 50th tree?
A42B42.85C45D4929 boys are standing in a line such that distance between any two consecutive boys is same. A teachr takes 7 seconds to reach from first boy to 15th boy. How much more time (in seconds) will he take to reach the 22nd boy?
A2.5B3C3.5D445 pillars are standing in a line such that distance between any two consecutive pillars is same. A car travelling with unifom speed of 72km/h takes 18 seconds to reach from 1st pole to 10th pole. What is the distance between 10th and 31st pole (in metres)?
A800B820C840D910
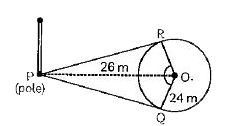
If six trees are to be planted along each tangential line segments at equal distances, find the distance between any two consecutive trees.
View SolutionTwo trees are standing along the opposite sides of a road. Distance between the two trees is 400 metres. There is a point on the road between the trees. The angle of depressions of the point from the top of the trees are 45∘ and 60∘. If the height of the tree which makes 45∘ angle is 200 metres, then what will be the height (in metres) of the other tree?
दो वृक्ष एक सड़क की विपरीत दिशा में खडे है। दोनों वृक्षों के मध्य की दूरी 400 मीटर है। दोनों वृक्षों के मध्य सड़क पर एक बिन्दु है। वृक्षों की चोटी से बिन्दु का अवनमन कोण 45∘ तथा 60∘ है। यदि वह वृक्ष जो 45∘ का कोण बनाता है की ऊँचाई 200 मीटर है, तो दूसरे वृक्ष की ऊंचाई (मीटर में) क्या हे?
View Solution45 pillars are standing in a line such that distance between any two consecutive pillars is same. A car travelling with unifom speed of 72km/h takes 18 seconds to reach from 1st pole to 10th pole. What is the distance between 10th and 31st pole (in metres)?
View SolutionThere are 20 poles with a constant distance between each pole. A car takes 24 seconds to reach the 12th pole. How much time will it take to reach the last pole ?
View SolutionA freely falling body takes t second to travel (1/x)th distance then time of descent is
View Solution
