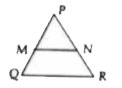
In ΔPQR, a line parallel to side QR cuts the side PQ and PR at points M and N respectively and point M divide PQ in the ratio of 1 : 2. If area of ΔPQR is 360 cm2, then what is the area (in cm2) of quadrilateral MNRQ?
160
320
120
96
To solve the problem, we will follow these steps:
Step 1: Understand the triangle and the ratio
We have triangle PQR with a line MN parallel to side QR. Point M divides side PQ in the ratio of 1:2. This means that if we let the length of PM be x, then the length of MQ will be 2x.
Step 2: Determine the ratio of the sides
Since M divides PQ in the ratio of 1:2, the total length of PQ can be expressed as:
PQ=PM+MQ=x+2x=3x
Thus, the ratio of PM to PQ is:
PMPQ=x3x=13
Step 3: Use the property of similar triangles
Triangles PMN and PQR are similar because MN is parallel to QR. The ratio of their areas is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
Area of △PMNArea of △PQR=(PMPQ)2=(13)2=19
Step 4: Calculate the area of triangle PMN
Given that the area of triangle PQR is 360 cm², we can find the area of triangle PMN:
Area of △PMN=19×Area of △PQR=19×360=40 cm2
Step 5: Calculate the area of quadrilateral MNRQ
To find the area of quadrilateral MNRQ, we subtract the area of triangle PMN from the area of triangle PQR:
Area of quadrilateral MNRQ=Area of △PQR−Area of △PMN=360−40=320 cm2
Final Answer
The area of quadrilateral MNRQ is 320 cm².
---
We have triangle PQR with a line MN parallel to side QR. Point M divides side PQ in the ratio of 1:2. This means that if we let the length of PM be x, then the length of MQ will be 2x.
Since M divides PQ in the ratio of 1:2, the total length of PQ can be expressed as:
PQ=PM+MQ=x+2x=3x
Thus, the ratio of PM to PQ is:
PMPQ=x3x=13
Triangles PMN and PQR are similar because MN is parallel to QR. The ratio of their areas is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
Area of △PMNArea of △PQR=(PMPQ)2=(13)2=19
Given that the area of triangle PQR is 360 cm², we can find the area of triangle PMN:
Area of △PMN=19×Area of △PQR=19×360=40 cm2
To find the area of quadrilateral MNRQ, we subtract the area of triangle PMN from the area of triangle PQR:
Area of quadrilateral MNRQ=Area of △PQR−Area of △PMN=360−40=320 cm2
The area of quadrilateral MNRQ is 320 cm².
Similar Questions
Knowledge Check
in ΔABC, a line parallel to side BC cuts the side AB and AC at points D and E respectively and also point D divide AB in the ratio of 1:4. If area of ΔABC is 200 cm2, then what is the area (in cm2) of quadrilateral DECB?
A192B50C120D96PQRSis a rectangle. Points A, B, C and D are the mid points of sides PQ,QR,RSandPSrespectively. If area of ΔPQR is 48cm2, then what is the area (in cm) of ΔBCD?
A24B6C16D12PQRS is a rectangle, A, B, C and D are the mid points of sides PQ, QR, RS and PS respectively. If area of ΔPQR is 48 cm2, then what is the area (in cm2) of ΔBCD?
A24B6C16D12
In ΔPQR, if S is any point on side QR, show that PQ+QR+RP>2PS.
View SolutionIn ΔABC, the line parallel to BC Intersects AB and AC at P and Q respectively. If AB:AP=5:3then AQ:QCis :
View SolutionIn ΔPQR,∠P:∠Q:∠R=2:2:5.A line parallel to QR is drawn which touches PQandPR at A and B respectively. What is the value of ∠PBA–∠PAB?
View SolutionIn the triangle PQR below, - S and T are 2 points on the sides RP and RQ respectively such that ST is parallel to PQ.
- The ratio of RT to TQ is 1:2.
The area of ΔRST = 100 sq. units.
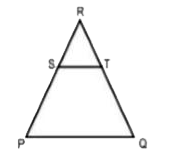
What is the area of PQTS?
View SolutionIn ΔPQR,PQ=PR=18cm, AB and AC are parallel to lines PR and PQ respectively. If A is the mid-point of QR, then what is the perimeter (in cm) of quadrilateral ABPC?
View Solution