In ΔPQR,SandT are the mid points of sides PQ and PR respectively. If ∠QPR=45∘and∠PRQ=55∘, then what is the value (in degrees) of ∠QST ?
80
85
90
100
The correct Answer is:A
To solve the problem step by step, we will analyze the triangle ΔPQR and the midpoints S and T.
Step 1: Identify the angles in triangle PQR
Given:
- ∠QPR=45∘
- ∠PRQ=55∘
To find ∠PQR, we use the fact that the sum of the angles in a triangle is 180∘.
∠PQR=180∘−∠QPR−∠PRQ
∠PQR=180∘−45∘−55∘=80∘
Step 2: Identify the midpoints
Let S be the midpoint of side PQ and T be the midpoint of side PR.
Step 3: Use the properties of midpoints
Since S and T are midpoints, by the Midpoint Theorem, the line segment ST is parallel to side QR and ST is half the length of QR.
Step 4: Determine the angles involving S and T
Since ST∥QR, the corresponding angles are equal. Therefore:
∠QST=∠PQR=80∘
Step 5: Find ∠QST
Now, we need to find ∠QST. Since S and T are midpoints, we can also analyze triangle QST.
Using the straight line property:
∠QST+∠PST=180∘
Where ∠PST is the angle at point P which is ∠QPR=45∘.
Thus:
∠QST+45∘=180∘
∠QST=180∘−45∘=135∘
However, we need to find ∠QST in relation to ∠PQR which we already found to be 80∘.
Final Step: Confirm the angle ∠QST
Since ST∥QR:
∠QST=∠PQR=80∘
Conclusion
Thus, the value of ∠QST is 80∘.
Given:
- ∠QPR=45∘
- ∠PRQ=55∘
∠PQR=180∘−45∘−55∘=80∘
Let S be the midpoint of side PQ and T be the midpoint of side PR.
Since S and T are midpoints, by the Midpoint Theorem, the line segment ST is parallel to side QR and ST is half the length of QR.
Since ST∥QR, the corresponding angles are equal. Therefore:
∠QST=∠PQR=80∘
Now, we need to find ∠QST. Since S and T are midpoints, we can also analyze triangle QST.
∠QST+∠PST=180∘
Where ∠PST is the angle at point P which is ∠QPR=45∘.
∠QST+45∘=180∘
∠QST=180∘−45∘=135∘
Since ST∥QR:
∠QST=∠PQR=80∘
Thus, the value of ∠QST is 80∘.
Similar Questions
In △PQR, S and T are mid-points of PQ and PR, respectively. If ∠QPR=75∘ and ∠PQR=40∘, then ∠TSQ is:
△PQR में, S और T क्रमशः PQ और PR के मध्य-बिंदु हैं, यदि ∠QPR=75∘ और ∠PQR=40∘ तो ∠TSQ है :
View SolutionIn ΔPQR, point S and T are on sides Pr and PQ such that ∠PQR=∠PST. If PT= 5 cm., PS = 3 cm. And TQ = 3 cm. then length of SR will be-
View Solution
Knowledge Check
The side QR of ΔPQR is produced to S. If ∠PRS=105∘ and ∠Q=(12)∠P, then what is the value of ∠P ?
A45B60C70D75PQRis a triangle such that PQ=PR.RSand QT are the medians to the sides PQandPR respectively. If the medians RS and GT intersect at right angle, then what is the value of (PQQR)2 ?
A32B52C2DNone of theseA circle passing through points Q and R of triangle PQR, cut the sides PQ and PR at point X and Y respectively. If PQ = PR, then what is the value (in degrees) of ∠PRQ+∠QXY ?
A120B150C240D180
PQR is a triangle such that PQ = PR. RS and QT are the median to the sides PQ and PR respectively. If the medians RS and QT intersect at right angle, then what is the value of (PQ/QR)2?
View SolutionIn A PQR, if PQ=PQ and L, M and N are the mid-points of the sides PQ, PR and RP respectively. Prove that LN=MN
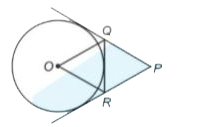
View SolutionIn the given figure, O is the centre of the circle. Circle has 3 tangents. If ∠QPR=450, then what is the calue (in degrees) of ∠QOR?
View SolutionIn a ΔPQR, the sides PQ and PR and are produced to S and T respectively. Bisectors of ∠SQRand∠QRT meet at the point O. If ∠P=66∘, then what is the value of ∠QOR?
View SolutionIf ΔPQRis right angled at Q,PQ=12and∠PRQ=30∘, then what is the value of QR?
View Solution
