Question

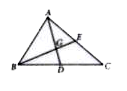
$\Delta ABC$ and $\Delta DBC$ are on the same base BC but on opposite sides of it. AD and BC intersect each other at O. If AO=a cm, DO=b cm and the area of $\Delta ABC=xc{m}^2$, then what is the area (in $c{m}^2$) of $\Delta DBC$?

Options

A. `(bx)/(a)`
B. `(a)/(b)x`
C. `(ab)/(2)x`
D. `((a+b))/(2)x`

Answer

A

Explanation

To find the area of triangle DBC given the area of triangle ABC, we can follow these steps:

1. Understand the Problem: We have two triangles, ABC and DBC, sharing the same base BC but positioned on opposite sides of it. The point O is where the lines AD and BC intersect.

2. Given Information:
- AO = a cm
- DO = b cm
- Area of triangle ABC = x cm²

3. Use the Area Ratio Theorem: The areas of triangles that share the same base and are between the same parallels are proportional to their heights. Here, the heights of triangles ABC and DBC from point A and D to line BC are AO and DO, respectively.

4. Set Up the Ratio:
\( \frac{\text{Area of } \Delta ABC}{\text{Area of } \Delta DBC} = \frac{AO}{DO} \)
Substituting the known values:
\( \frac{x}{\text{Area of } \Delta DBC} = \frac{a}{b} \)

5. Cross-Multiply to Solve for Area of DBC:
\( x \cdot b = \text{Area of } \Delta DBC \cdot a \)

6. Isolate the Area of DBC:
\( \text{Area of } \Delta DBC = \frac{b \cdot x}{a} \)

Final Answer:
The area of triangle DBC is \(\frac{bx}{a}\) cm².