Two parallel chords on the same sideof the centre of a circle are 12 cm and 20 cm long the radius of the circle is 5√13cm. What is the distance (in cm) between the chord?
2
3
2.5
1.5
The correct Answer is:A
To solve the problem, we need to find the distance between two parallel chords in a circle. Here’s a step-by-step breakdown of the solution:
Step 1: Understanding the Problem
We have a circle with a radius of 5√13 cm, and two parallel chords of lengths 12 cm and 20 cm. We need to find the distance between these two chords.
Step 2: Drawing the Circle and Chords
1. Draw a circle with center O.
2. Draw two parallel chords AB and CD such that AB=20 cm and CD=12 cm. Both chords are on the same side of the center O.
Step 3: Finding the Distances from the Center to Each Chord
Using the property that the perpendicular from the center of the circle to a chord bisects the chord, we can find the distances from the center O to each chord.
For Chord AB:
1. Since AB=20 cm, the half-length AM=MB=10 cm.
2. In triangle OAM (where M is the midpoint of chord AB):
- Hypotenuse OA=5√13 cm (radius).
- Base AM=10 cm.
- Let OC be the perpendicular distance from O to chord AB.
Using the Pythagorean theorem:
OA2=OC2+AM2
(5√13)2=OC2+102
325=OC2+100
OC2=325−100=225
OC=√225=15 cm
For Chord CD:
1. Since CD=12 cm, the half-length CN=ND=6 cm.
2. In triangle OCN (where N is the midpoint of chord CD):
- Hypotenuse OC=5√13 cm (radius).
- Base CN=6 cm.
- Let OD be the perpendicular distance from O to chord CD.
Using the Pythagorean theorem:
OC2=OD2+CN2
(5√13)2=OD2+62
325=OD2+36
OD2=325−36=289
OD=√289=17 cm
Step 4: Finding the Distance Between the Chords
Now, we can find the distance between the two chords:
Distance between the chords=OD−OC=17−15=2 cm
Final Answer
The distance between the two chords is 2 cm.
---
We have a circle with a radius of 5√13 cm, and two parallel chords of lengths 12 cm and 20 cm. We need to find the distance between these two chords.
1. Draw a circle with center O.
2. Draw two parallel chords AB and CD such that AB=20 cm and CD=12 cm. Both chords are on the same side of the center O.
Using the property that the perpendicular from the center of the circle to a chord bisects the chord, we can find the distances from the center O to each chord.
1. Since AB=20 cm, the half-length AM=MB=10 cm.
2. In triangle OAM (where M is the midpoint of chord AB):
- Hypotenuse OA=5√13 cm (radius).
- Base AM=10 cm.
- Let OC be the perpendicular distance from O to chord AB.
OA2=OC2+AM2
(5√13)2=OC2+102
325=OC2+100
OC2=325−100=225
OC=√225=15 cm
1. Since CD=12 cm, the half-length CN=ND=6 cm.
2. In triangle OCN (where N is the midpoint of chord CD):
- Hypotenuse OC=5√13 cm (radius).
- Base CN=6 cm.
- Let OD be the perpendicular distance from O to chord CD.
OC2=OD2+CN2
(5√13)2=OD2+62
325=OD2+36
OD2=325−36=289
OD=√289=17 cm
Now, we can find the distance between the two chords:
Distance between the chords=OD−OC=17−15=2 cm
The distance between the two chords is 2 cm.
Similar Questions
Two parallel chords on the same side of the centre of a circle are 12 cm and 20 cm long and the radius of the circle is 5√13 cm. What is the distance (in cm) between the chords ?
किसी वृत्त के केंद्र के एक ही तरफ दो समानांतर जीवाएं 12 सेमी और 20 सेमी लंबी हैं तथा वृत्त की त्रिज्या 5√13 सेमी की है| जीवाओं के बीच की दूरी (सेमी में ) ज्ञात करें |
View SolutionAB and CD are two parallel chords on the opposite sides of the centre of the circle. If AB =10cm CD =24 cm and the radius of the circle is 13 cm, the distance between the chords is
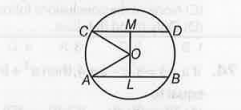
(A) 17 cm (B) 15 cm (C ) 16 cm (D) 18 cm
View Solution
Knowledge Check
Two parallel chords are on one side of the centre of a circle. The length of the two chords is 24 cm and 32 cm. If the distance between the two chords is 8 cm, then what is the area (in cm2) of the circle?
A724.14B832.86C924.12D988.32AB=8cmandCD=6cmare two parallel chords on the same side of the centre of a circle. The distance between them is 1 cm. The radius of the circle is
A5 cmB4 cmC3 cmD2 cmIn a circle, there are two chords opposite to the centre of the circle. The length of one chord and the radius of the circle is 6 cm and 5 cm respectively, and the distance between both the chords is 7 cm. Find the length of the second chord.
Aa) 8 cmBb) 10 cmCc) 6 cmDd) 14 cm
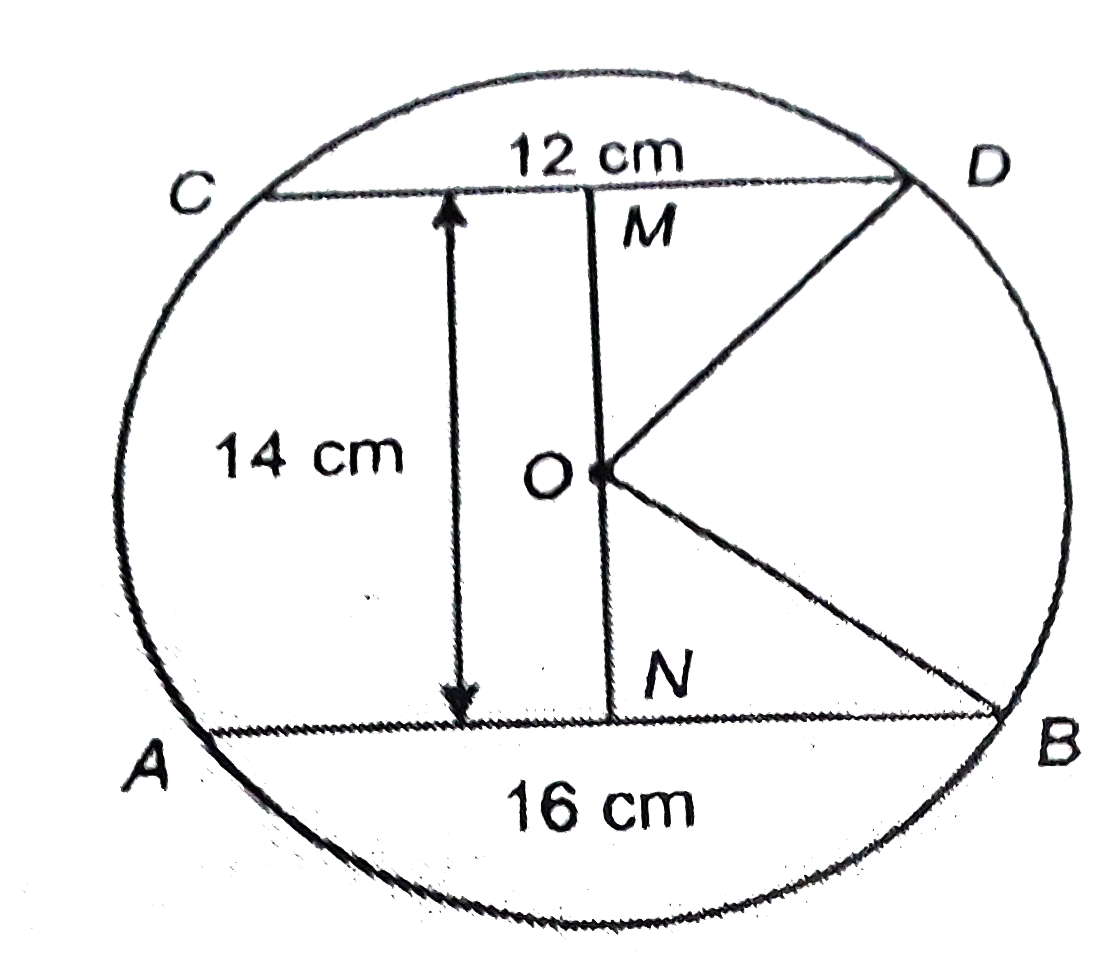
In the adjoining figure ,AB and CD are two parallel chords of a circle with centre O , whose length are 16 cm and 12 cm respectively. Find the radius of the circle if the distance between them is 14 cm.
View SolutionThe length of two parallel chords of a circle are 6 cm and 8 cm . The radius of the circle is 5 cm. Find the distance btween them if :
(i) chords are on the same side of the centre.
(ii) chords are on the opposite side of the centre.
View SolutionTwo parallel chords are on one side of the centre of a circle. The length of the two chords is 24 cm and 32 cm. If the distance between the two chords is 8 cm, then what is the area (in cm2) of the circle?
View SolutionIn a circle of radius 13 cm, AB and CD are two equal and chords of lengths 24 cm each .What is the distance between the chords ?
View SolutionThe radius of a circle is 13 cm and the length of one of its chords is 10 cm . The distance of the chord from the centre is
View Solution
