In the given figure, ABC is a right angled triangle. ∠ABC=900 and ∠ACB=600. If the radius of the smaller circle is 2 cm, then what is the radius (in cm) of the larger circle?
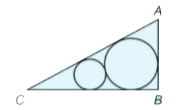
4
6
4.5
7.5
The correct Answer is:B
Step by step video & image solution for In the given figure, ABC is a right angled triangle. /_ ABC=90^0 and /_ ACB=60^0. If the radius of the smaller circle is 2 cm, then what is the radius (in cm) of the larger circle? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
In the given figure, ABC is a right angled triangle. ∠ABC=90∘and∠ACB=60∘. If the radius of the smaller circle is 2 cm, then what is the radius (in cm) of the larger circle?
View SolutionABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :

View Solution
Knowledge Check
In the given figure, ABC is a right angled triangle. ∠ABC=90∘and∠ACB=60∘. If the radius of the smaller circle is 2 cm, then what is the radius (in cm) of the larger circle?
 A4B6C4.5D7.5
A4B6C4.5D7.5ABCis a right angled triangle. ∠BAC=90∘ and ∠ACB=60∘. What is the ratio of the circum radius of the triangle to the side AB ?
A1:2B1:13C2:13D2:3ABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
 A1 cmB1.25 cmC1.5 cmDnone of these
A1 cmB1.25 cmC1.5 cmDnone of these
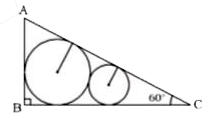
In a right angle triangle ABC. ∠B is a right angle and ∠C=60∘. If radius of small circle is 1 cm. then find R = ?
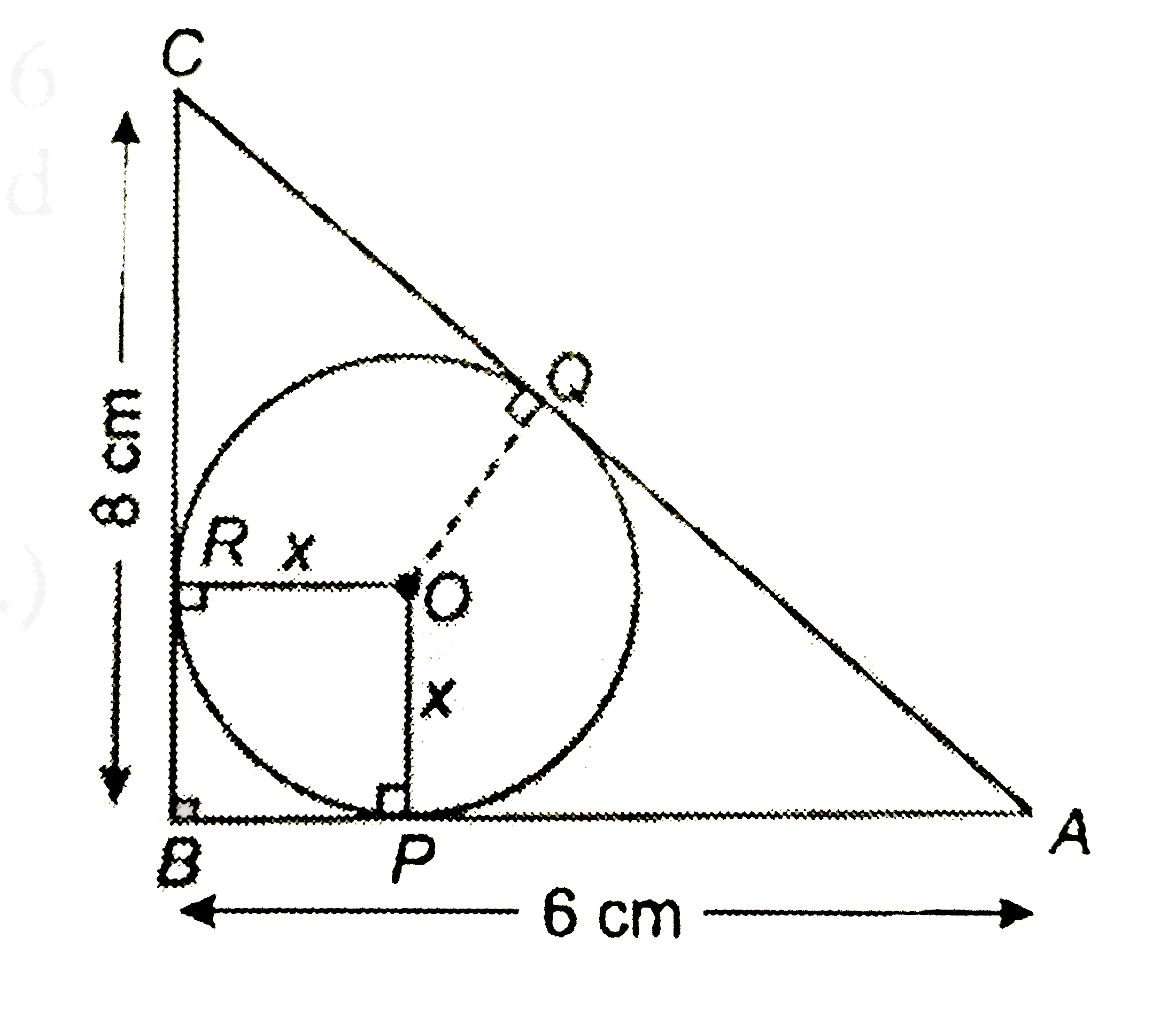
View SolutionIn the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
View SolutionIn a right angled triangle ABCABC=90∘,ACB=30∘ and AB=8cm. Find the length of the other sides of the triangle.
View SolutionABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
View SolutionIn the figure , triangle ABC is isosceles in which AB = AC = 6 cm . If the radius of circle is 9 cm then what is the area of the triangle?
View Solution
