In the given figure, four identical semicircles are drawn in a quadrant. XA=7cm. What is the area (in cm2) of shaded region ?
70
140
77
84
The correct Answer is:D
Step by step video & image solution for In the given figure, four identical semicircles are drawn in a quadrant. XA=7cm. What is the area (in cm^(2)) of shaded region ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Similar Questions
In the given figure, four identical semicircles are drawn in a quadrant. XA = 7 cm. What is the area (in cm2) of shaded region?
दी गई आकृति में, चार समरूप अर्धवृत्तों को एक वृत्त के चतुर्थ भाग में बनाया गया है। XA=7 से.मी. है। छायांकित भाग का क्षेत्रफल (सेमी2 में) क्या है?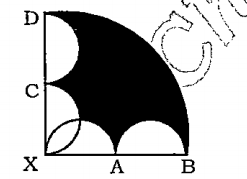
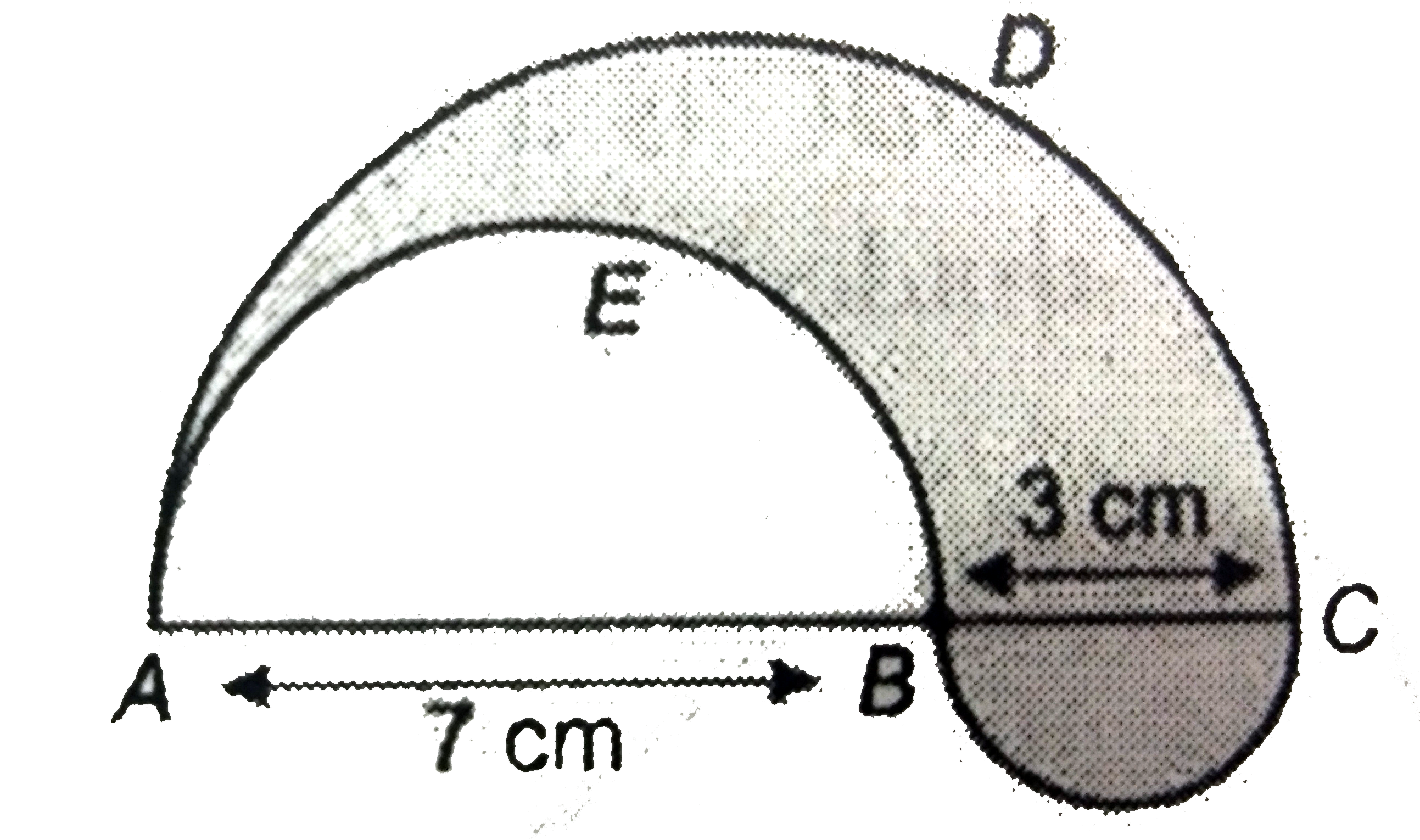
View SolutionIn the given figure, three semicircles are drawn of diameter 10 cm, 7 cm and 3 cm, respectively Find the perimeter of shaded regions (Use π=3.14)
View Solution
Knowledge Check
- Question 1 - Select One
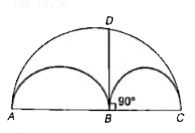
In the adjoining figure there are three semicircles in which BC=6 cm and BD=6√3 cm. What is the area of the shaded region ( in cm) :
A12πB9πC27πD28π
In the given figure, two squares of sides 8cm and 20cm are given. What is the area (in cm2) of the shaded part ?
View SolutionIn the given figure, AB AE, EF, FG and GB are semicircles. AB = 56 cm. and AE = EF = FG = GB. What is the area (in cm2.) of the shaded region ?
View SolutionIn the given figure, ABCD and BEFG are squares of sides 8cm. And 6 cm respecitively. What is the area (in cm2) of the shaded region ?
View SolutionIn the given figure, a square OABC has been inscribed in the quadrant OPBQ .If OA=20cm then the area of the shaded region is [take π=3.14]
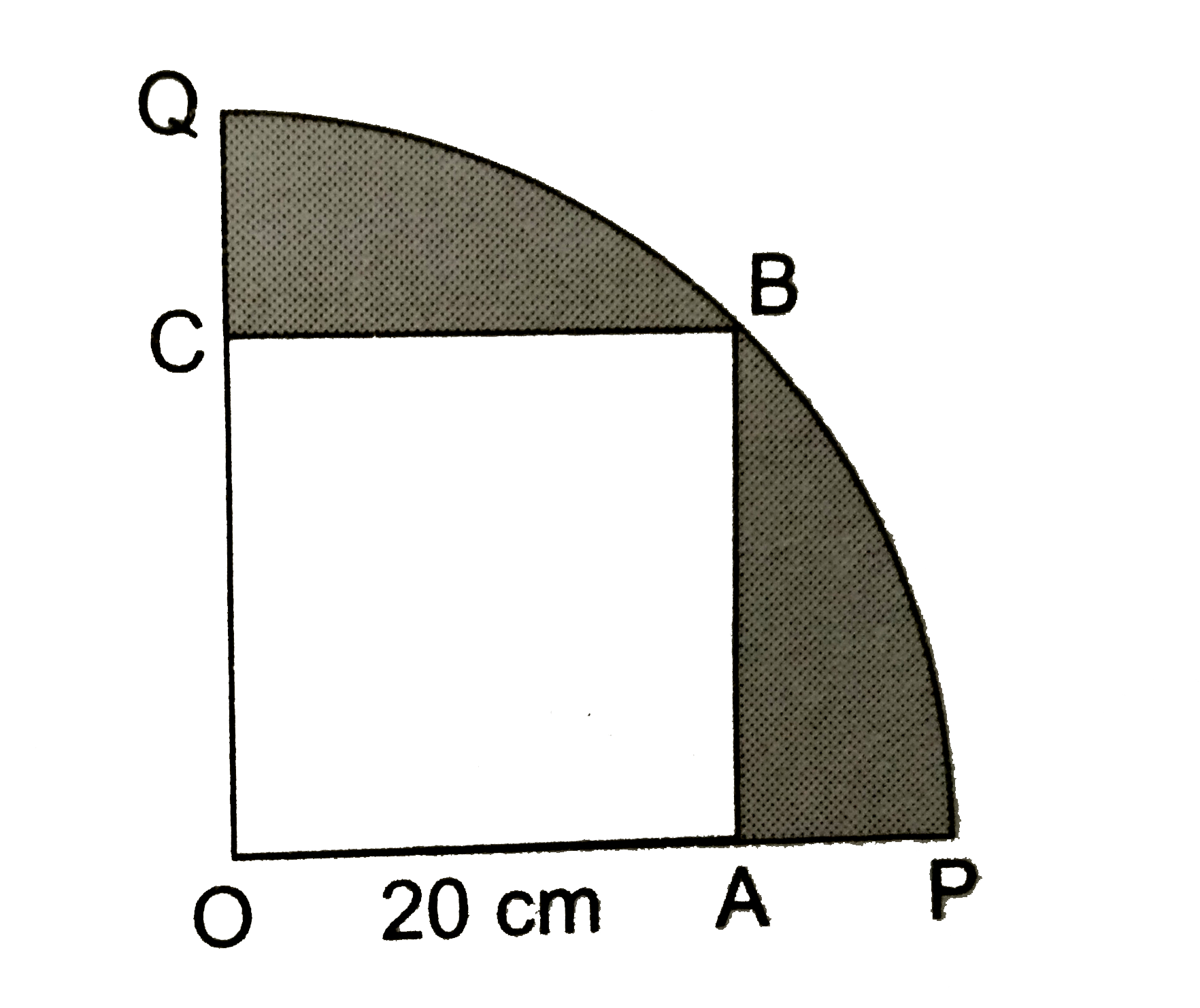
View SolutionIn the given figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 15 cm, find the area of the shaded region. (Use π = 3.14)
View SolutionThe given figure shows a circle inscribed in a square of side 14 cm.
What is the area of the shaded region?View SolutionIn the given figure, ABCD is a square of side 14cm.Semicircles are drawn with each side of square as diameter. Find the area of the shaded region.
View Solution