In which period was the legendary Victoria Terminus station (currently Chhatrapati Shivaji Maharaj Terminus), mumbai built?
1843 to 1853
1911 to 1921
1933 to 1943
1878 to 1888
The correct Answer is:D
Similar Questions
Knowledge Check
In which period was the legendary Victoria Terminus Station (currently Chhtarpati Shivaji Maharaj Terminus), Mumbai built?
Aa.1878 to 1888Bb.1843 to 1853Cc.1933 to 1943Dd.1911 to 1921Victoria, Terminus is presently known as—
AChattrapati Shivaji Terminus,BKolkata Terminus,CBombay High,DChennai Terminus.Which of the following coins was NOT a silver coin in the Kingdom of Chhatrapati Shivaji?
ARupayaBLariCTakaDRuka
A large number of molecular rearrangements involve anionotropic migration of a group to an adjacent atom with incomplete octet. The migration group may either detach from the migration origin and then form bond with the migration terminus or may remain partly bonded to both migration origin and terminus to form a bridged ion intermediate. similar to the electron deficent carbon such as carbocation and carbene intermediates, electron-deficient nitrogen species are known in which the nitrogen bears a positive charge or the nitrogen has an open sextet of electrons, i.e., a nitrene.
Q. Which of the following is stable product for given reaction?
HO−CH2−CH2−CH2−CH2−OHH+−−→ ?
View SolutionRead the following text and answer the following questions on the basis of the same:
Shunt resistance: The ammeter shunt is the device which provides the low resistance path to the flow of current. It is connected in parallel with the ammeter. In some ammeter the shunt is in-built inside the instrument while in others it is externally connected to the circuit. Manganin and Constantan are used for making the shunt of DC and AC ammeter respectively.
Ammeters are designed for measurement of low current. For measuring high current, the shunt is connected in parallel to the ammeter. The significant portion of the current passes to the shunt because of the low resistance path and little amount of current passes through the ammeter.
The shunt is connected in parallel to the ammeter because of which the voltage drops across the meter and shunt remain the same. Thus, the movement of the pointer is not affected by the shunt.
Let us consider that the current to be measured is I. The circuit has ammeter and shunt connected parallel to each other. The ammeter is designed for measurement of small current say, Im. The magnitude of the current I passes through the meter is very high, and it will burn the meter. So, for measuring the current I the shunt is required in the circuit.
As the shunt connects in parallel with the ammeter, thus the same voltage drops occur between them:
IShRSH=ImRm
∴RSH=ImRm/ISH
Shunt current ISH=I−Im
So, RSH=ImRm/(I−Im)
∴I/Im=1+(Rm/RSH)
The ratio of the total current to the current required for the movement of the ammeter coil is called the multiplying power of the shunt.
∴ The multiplying power =m=I/Lm
RSH=Rm/(m−1)
The following are the requirements of the shunt.
• The resistance of the shunt should remain constant with time.
• The temperature of the material-should remain same even though substantial current flows through the circuit.
Materials used for making shunt of DC and AC ammeter are respectively
View SolutionArchaeologists seeking the location of a legendary siege and destruction of city are excavating in several possible places, including a middle and a lower layer of a large mound. The bottom of the middle layer contains some pieces of pottery of type 3 , known to be from a later period than the time of the destruction of the city, but lower layer does not.
Which of the following hypotheses is best supported by the evidence above ?
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
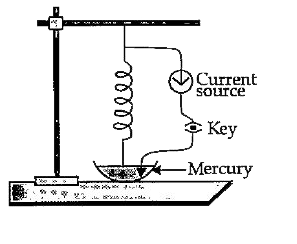
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
Why the spring shrinks in Roget's spiral?
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
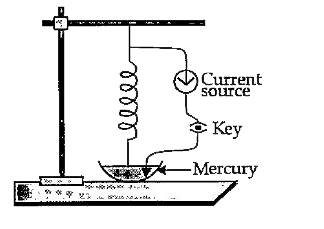
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
What else can be used instead of mercury in Roget's spiral?
View Solution
