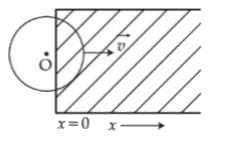
A constant magnetic field of 1 T is applied in the x>0 region. A metallic circular ring of radius 1 m is moving with a constant velocity of 1 m/s along the x-axis. At t=0 s, the centre O of the ring is at x=-1 m. What will be the value of the induced emf in the ring at t=1s? (Assume the velocity of the ring does not change.)
1 V
0 V
2πV
2 V
Step by step video & image solution for A constant magnetic field of 1 T is applied in the x gt 0 region. A metallic circular ring of radius 1 m is moving with a constant velocity of 1 m/s along the x-axis. At t=0 s, the centre O of the ring is at x=-1 m. What will be the value of the induced emf in the ring at t=1s? (Assume the velocity of the ring does not change.) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A ring of mass 1kg and radius 1m is moving with a velocity of 1m/s by rolling on a frictionless inclined plane. The total kinetic energy of the ring is
View SolutionUniform inward magnetic field B = 0.5 T exists in a circular region of radius 5m. At t = 0 one metal ring of radius 5 m completely encloses the magnetic field. Now ring starts a moving with constant velocity 1m/s. Find the emf in volts induced in the ring at t=6s.
View Solution
Knowledge Check
vx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
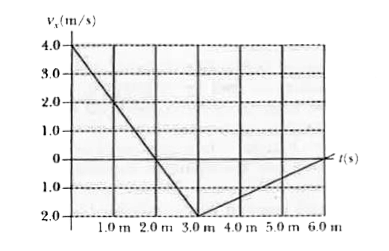 A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A−2.0 mB+2.0 mC+1.0 mD−1.0 mA thin circular ring of mass m and radius R is rotating about its axis with a constant angular velocity ω. Two objects each of mass M are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity ω'=
Aω(m+2M)mBω(m−2M)(m+2M)Cωm(m+M)Dωm(m+2M)A thin circular ring of mass M and radius r is rotating about its axis with constant angular velocity ω . Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring . The ring now rotates with angular velocity given by
A(M+2m)ω2mB2MωM+2mC(M+2m)ωMDMωM+2m
A ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA horizontal ring of radius r=12m is kept in a vertical constant magentic field 1T. The ring is collapsed from maximum area to zero area in 1s. Then the emf induced in the ring is
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity ω. The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring. The ring will now rotate with an angular velocity
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?

View Solution
