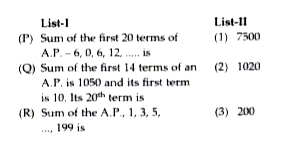Match List - I with List - II.
List-IList-II(a)Torque(i)MLT−1(b)Impulse(ii)MT−2(c )Tension(iii)ML2T−2(d)Surface Tenion(iv)MLT−2
(a)-(ii),(b)-(i),(c )-(iv),(d)-(iii)
(a)-(iii),(b)-(iv),(c )-(i),(d)-(ii)
(a)-(iii),(b)-(i),(c )-(iv),(d)-(ii)
(a)-(i),(b)-(iii),(c )-(iv),(d)-(ii)
The correct Answer is:C
To solve the problem of matching List-I with List-II based on the dimensions of physical quantities, we will analyze each quantity one by one and derive their dimensions.
Step 1: Analyze Torque
- Torque (τ) is defined as the product of force (F) and the distance (r) from the pivot point, which can be expressed as:
τ=F⋅r
- The unit of force (F) is given by Newton (N), which is equivalent to kg⋅m/s2.
- Therefore, the unit of torque can be expressed as:
Torque=Force×Distance=N⋅m=(kg⋅m/s2)⋅m=kg⋅m2/s2
- The dimensions of torque are:
(τ)=ML2T−2
Step 2: Analyze Impulse
- Impulse (J) is defined as the change in momentum, which can also be expressed as:
J=F⋅Δt
- The unit of impulse is the same as the unit of momentum, which is given by:
Momentum=mass×velocity=kg⋅(m/s)=kg⋅m/s
- Therefore, the dimensions of impulse are:
(J)=MLT−1
Step 3: Analyze Tension
- Tension (T) is a force, and thus its unit is the same as that of force:
T=Force=N=kg⋅m/s2
- The dimensions of tension are:
(T)=MLT−2
Step 4: Analyze Surface Tension
- Surface tension (σ) is defined as force per unit length:
σ=ForceLength=Nm=kg⋅m/s2m=kg/s2
- The dimensions of surface tension are:
(σ)=MT−2
Step 5: Match the Lists
Now that we have the dimensions for each quantity, we can match them with List-II:
- (a) Torque → (iii) ML2T−2
- (b) Impulse → (i) MLT−1
- (c) Tension → (ii) MLT−2
- (d) Surface Tension → (iv) MT−2
Final Matching:
- (a) Torque → (iii)
- (b) Impulse → (i)
- (c) Tension → (ii)
- (d) Surface Tension → (iv)
- Torque (τ) is defined as the product of force (F) and the distance (r) from the pivot point, which can be expressed as:
τ=F⋅r
- The unit of force (F) is given by Newton (N), which is equivalent to kg⋅m/s2.
- Therefore, the unit of torque can be expressed as:
Torque=Force×Distance=N⋅m=(kg⋅m/s2)⋅m=kg⋅m2/s2
- The dimensions of torque are:
(τ)=ML2T−2
- Impulse (J) is defined as the change in momentum, which can also be expressed as:
J=F⋅Δt
- The unit of impulse is the same as the unit of momentum, which is given by:
Momentum=mass×velocity=kg⋅(m/s)=kg⋅m/s
- Therefore, the dimensions of impulse are:
(J)=MLT−1
- Tension (T) is a force, and thus its unit is the same as that of force:
T=Force=N=kg⋅m/s2
- The dimensions of tension are:
(T)=MLT−2
- Surface tension (σ) is defined as force per unit length:
σ=ForceLength=Nm=kg⋅m/s2m=kg/s2
- The dimensions of surface tension are:
(σ)=MT−2
Now that we have the dimensions for each quantity, we can match them with List-II:
- (a) Torque → (iii) ML2T−2
- (b) Impulse → (i) MLT−1
- (c) Tension → (ii) MLT−2
- (d) Surface Tension → (iv) MT−2
- (a) Torque → (iii)
- (b) Impulse → (i)
- (c) Tension → (ii)
- (d) Surface Tension → (iv)
Topper's Solved these Questions
Similar Questions
Knowledge Check
Match the List-I with List-II:
 A(I)(II)(III)(IV)1245B(I)(II)(III)(IV)5436C(I)(II)(III)(IV)2611D(I)(II)(III)(IV)6251
A(I)(II)(III)(IV)1245B(I)(II)(III)(IV)5436C(I)(II)(III)(IV)2611D(I)(II)(III)(IV)6251Match the List-I with List-II:
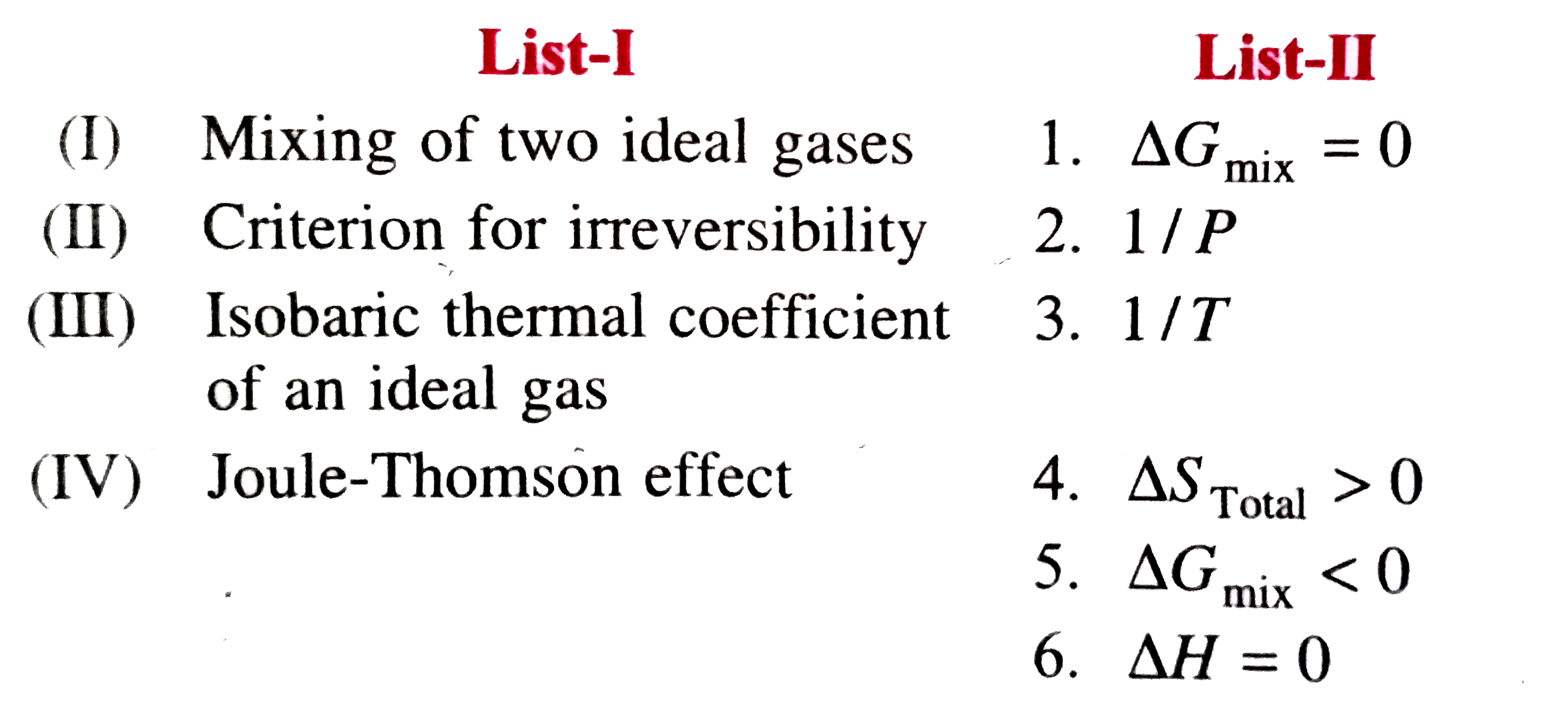 A(I)(II)(III)(IV)1245B(I)(II)(III)(IV)5436C(I)(II)(III)(IV)2615D(I)(II)(III)(IV)6251
A(I)(II)(III)(IV)1245B(I)(II)(III)(IV)5436C(I)(II)(III)(IV)2615D(I)(II)(III)(IV)6251Match the List-I with List-II:
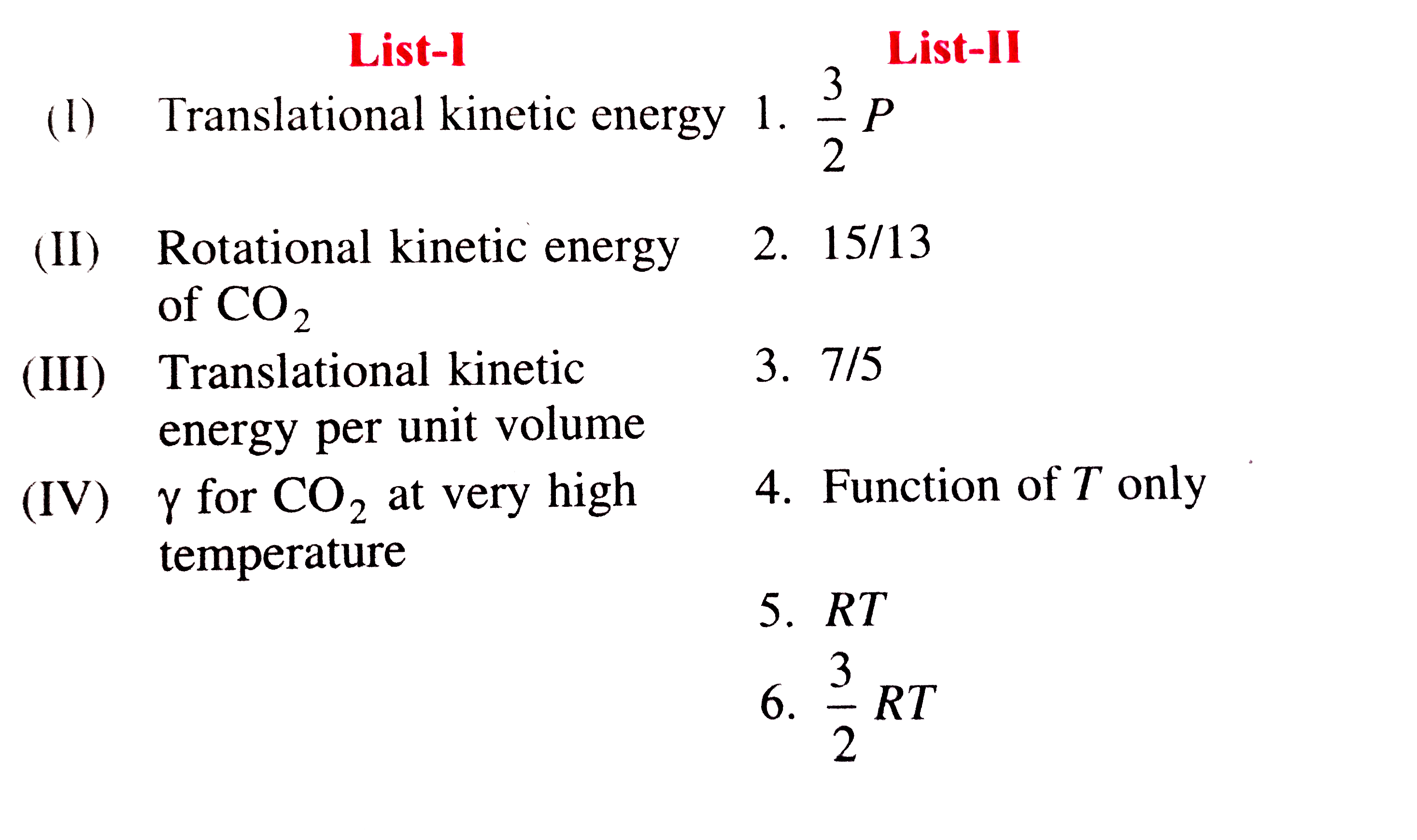 A(I)(II)(III)(IV)3451B(I)(II)(III)(IV)4512C(I)(II)(III)(IV)5623D(I)(II)(III)(IV)6134
A(I)(II)(III)(IV)3451B(I)(II)(III)(IV)4512C(I)(II)(III)(IV)5623D(I)(II)(III)(IV)6134