A particle of mass 1 kg is hanging from a spring of force constant 100 Nm1 . The mass is pulled slightly downward and released so that it executes free simple harmonic motion with time period T. The time when the kinetic energy and potential energy of the system will become equal, is Tx The value of x is_______
The correct Answer is:8
To solve the problem, we need to find the time at which the kinetic energy (KE) and potential energy (PE) of a mass-spring system are equal during simple harmonic motion (SHM).
1. Identify the parameters:
- Mass (m) = 1 kg
- Spring constant (k) = 100 N/m
2. Calculate the time period (T) of the SHM:
The formula for the time period T of a mass-spring system is given by:
T=2π√mk
Substituting the values:
T=2π√1100=2π√0.01=2π⋅0.1=0.2π seconds
3. Formulas for kinetic and potential energy:
In SHM, the potential energy (PE) and kinetic energy (KE) can be expressed as:
- Potential Energy:
PE=12kx2
- Kinetic Energy:
KE=12mv2
where v is the velocity of the mass.
4. Expressing PE and KE in terms of displacement:
For SHM, the displacement x can be expressed as:
x=Asin(ωt)
where A is the amplitude and ω=2πT.
The velocity v is given by:
v=dxdt=Aωcos(ωt)
5. Substituting into the energy equations:
- Potential Energy becomes:
PE=12k(Asin(ωt))2=12kA2sin2(ωt)
- Kinetic Energy becomes:
KE=12m(Aωcos(ωt))2=12mA2ω2cos2(ωt)
6. Setting KE equal to PE:
To find when KE = PE:
12kA2sin2(ωt)=12mA2ω2cos2(ωt)
Canceling 12A2 from both sides gives:
ksin2(ωt)=mω2cos2(ωt)
7. Using the relationship ω2=km:
Substitute ω2:
ksin2(ωt)=ksin2(ωt)cos2(ωt)
This simplifies to:
sin2(ωt)=cos2(ωt)
This implies:
tan2(ωt)=1⇒tan(ωt)=1⇒ωt=π4
8. Solving for time t:
Substitute ω=2πT:
2πTt=π4⇒t=T8
9. Finding the value of x:
Since t=Tx, we have:
x=8
Final Answer:
The value of x is 8.
- Mass (m) = 1 kg
- Spring constant (k) = 100 N/m
The formula for the time period T of a mass-spring system is given by:
T=2π√mk
Substituting the values:
T=2π√1100=2π√0.01=2π⋅0.1=0.2π seconds
In SHM, the potential energy (PE) and kinetic energy (KE) can be expressed as:
- Potential Energy:
PE=12kx2
- Kinetic Energy:
KE=12mv2
where v is the velocity of the mass.
For SHM, the displacement x can be expressed as:
x=Asin(ωt)
where A is the amplitude and ω=2πT.
v=dxdt=Aωcos(ωt)
- Potential Energy becomes:
PE=12k(Asin(ωt))2=12kA2sin2(ωt)
- Kinetic Energy becomes:
KE=12m(Aωcos(ωt))2=12mA2ω2cos2(ωt)
To find when KE = PE:
12kA2sin2(ωt)=12mA2ω2cos2(ωt)
Canceling 12A2 from both sides gives:
ksin2(ωt)=mω2cos2(ωt)
Substitute ω2:
ksin2(ωt)=ksin2(ωt)cos2(ωt)
This simplifies to:
sin2(ωt)=cos2(ωt)
This implies:
tan2(ωt)=1⇒tan(ωt)=1⇒ωt=π4
Substitute ω=2πT:
2πTt=π4⇒t=T8
Since t=Tx, we have:
x=8
The value of x is 8.
Topper's Solved these Questions
Similar Questions
A particle of mass 40 g executes a simple harmonic motion of amplitude 2.0 cm. If the time period is 0.20 s, find the total mechanical energy of the system.
View SolutionA mass M is suspended from a spring of negligible mass. The spring is pulled a little then released, so that the mass executes simple harmonic motion of time period T. If the mass is increased by m, the time period becomes 5T3. Find the ratio of m/M.
View Solution
Knowledge Check
A particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
ATB2TC4TDT2A mass M is suspended from a spring of negiliglible mass the spring is pulled a little and then released so that the mass executes simple harmonic oscillation with a time period T If the mass is increases by m the time period because (54T),The ratio of mM is
A9/16B25/16C4/5D5/4A particle is executing simple harmonic motion with a time period T. At time t=0, it is at its position of equilibium. The kinetice energy -time graph of the particle will look like
A B
B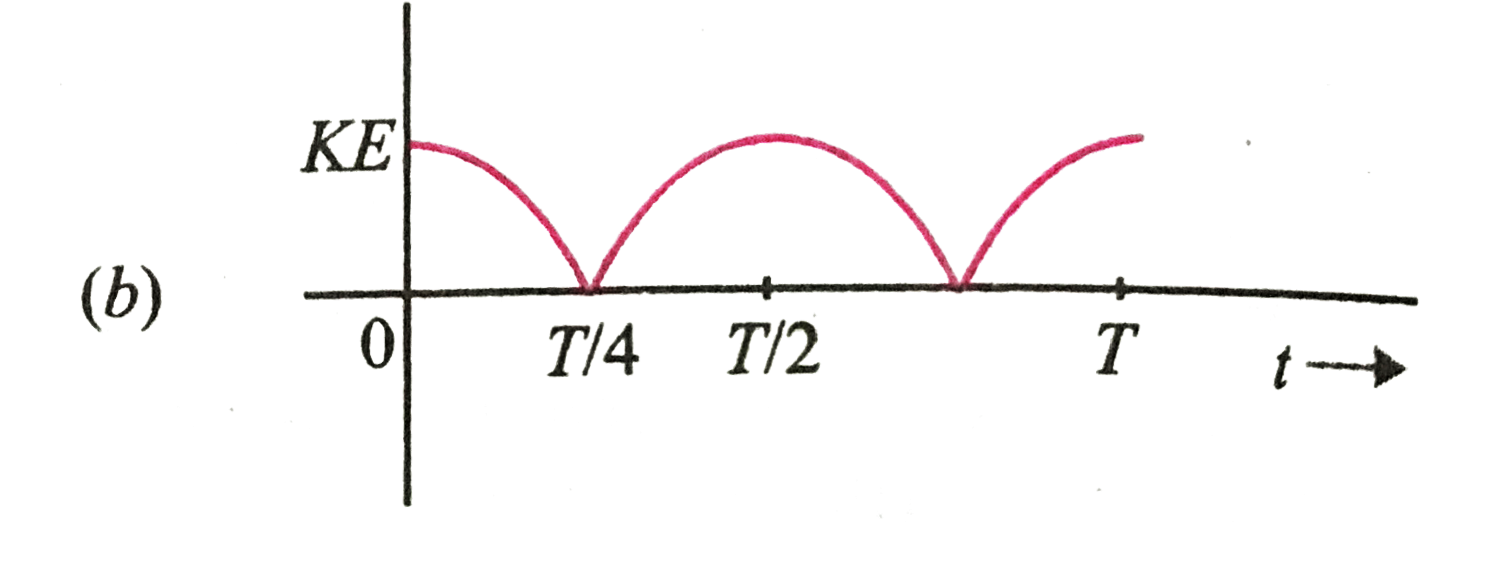 C
C D
D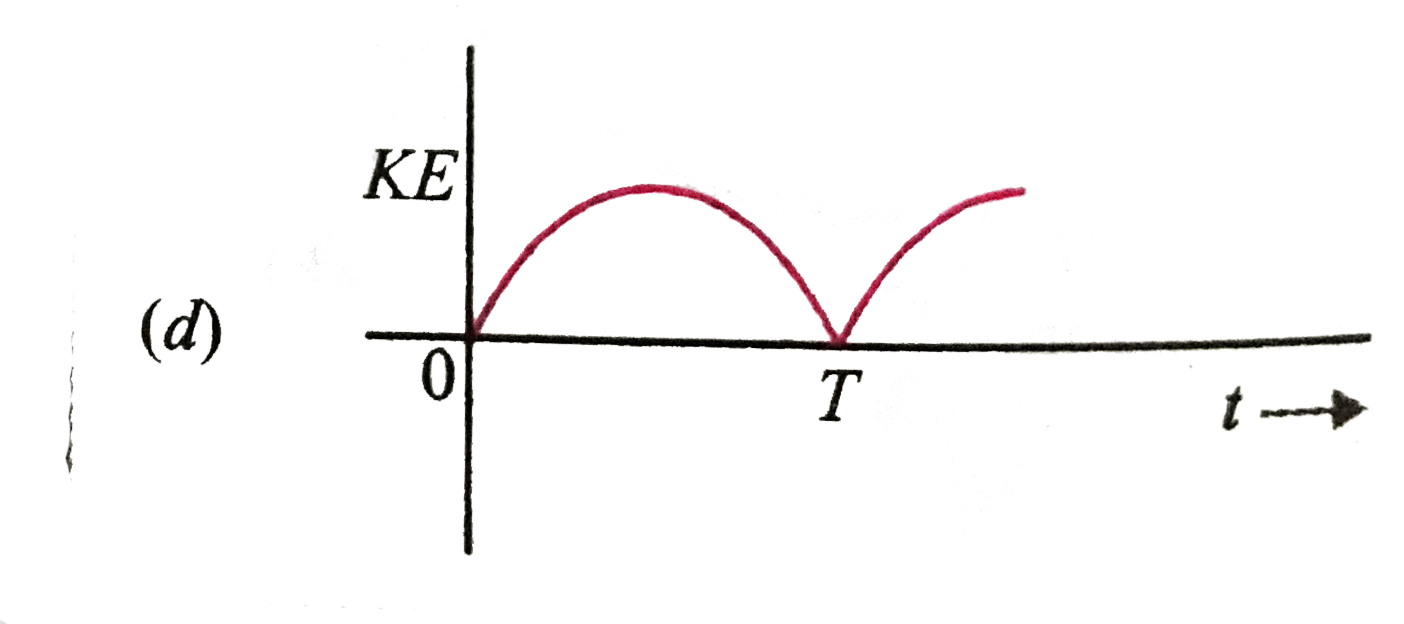
A particle is executing simple harmonic motion with amplitude A. When the ratio of its kinetic energy to the potential energy is 14 , its displacement from its mean position is
View SolutionA particle executes simple harmonic motion with a time period of 16s. At time t=4s its velocity is 4ms−1. Find its amplitute of motion.
View SolutionA solid sphere of mass M and Radius R is attached to a massless spring of force constant k as shown in the figure. The cylinder is pulled towards right slightly and released so that it executes simple harmonic motion of time period. If the cylinder rolls on the horizontal surface without slipping, calculate its time period of oscillation.

View SolutionA body of mass m = 2kg hangs from three springs, each of spring constant 1875 N/m, as shown in the figure. If the mass is slightly displaced and let go, the system will oscillate with time period
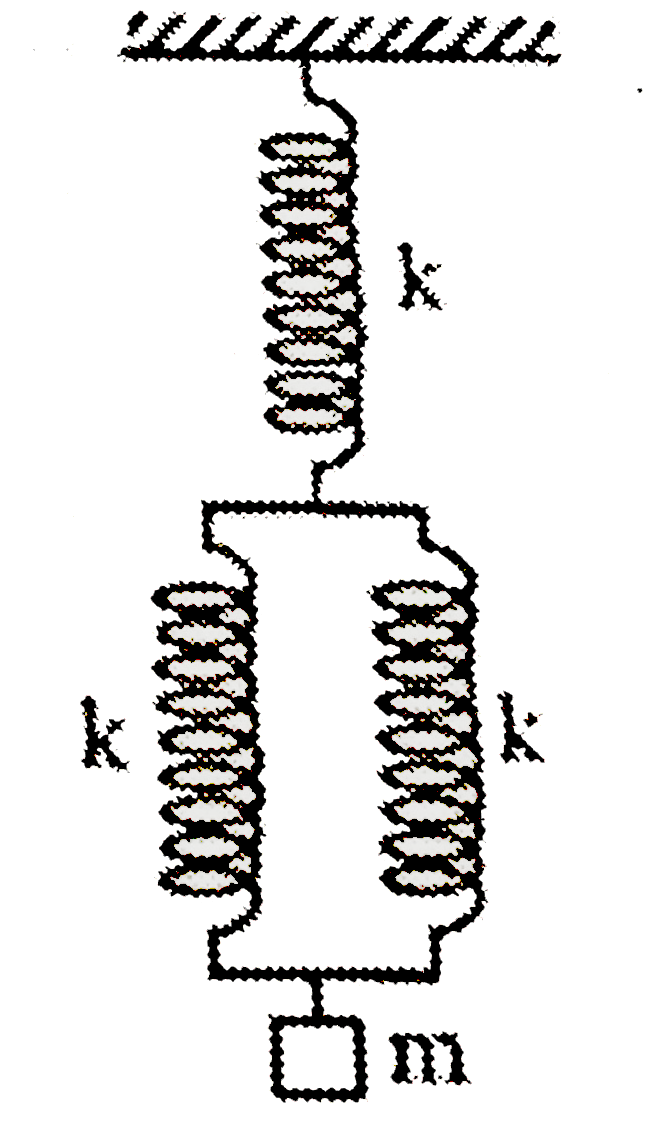
View SolutionA particle starts oscillating simple harmonically from its equilibrium position then, the ration of kinetic energy and potential energy of the particle at the time T/12 is: (T=time period)
View Solution
