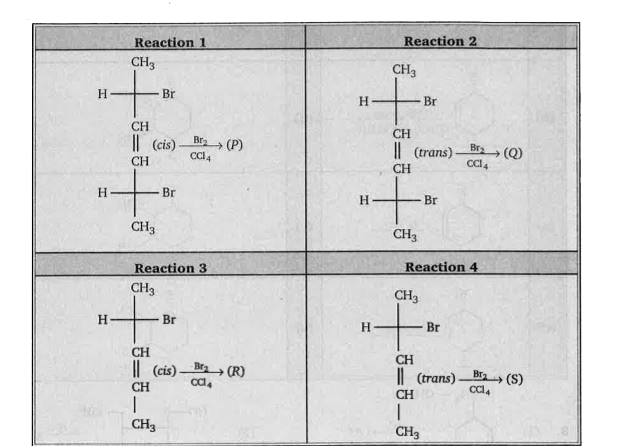
How many products are formed by sum of P,Q,R,S ?Solution in Kannada
The correct Answer is:P+Q+R+S = 8
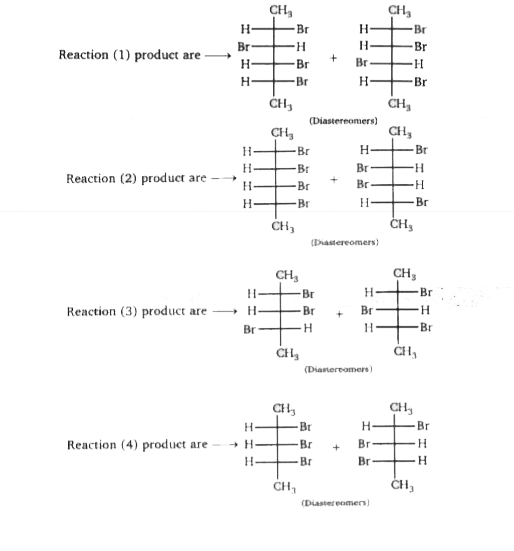
Sum of products (P + Q + R+S) = 8
Topper's Solved these Questions
Similar Questions
In each reagent box write a letter designating the best reagent and condition selected from the above list of reagents.
03:11View Solution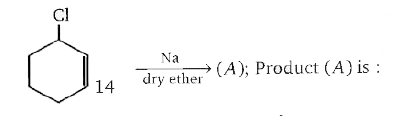
02:19View SolutionComplete the following reaction
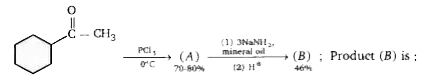03:54View SolutionA = [[p,q],[r,s]] where p, q, r and s are positive integers. If A is symmetric matrix, |A|=20 and p = q, then find how many values are possible for s.
01:26View SolutionIf the centroid of the triangle formed by (p,q),(q,r),(r,s) is (0,0) then p^(3)+q^(3)+r^(3)=
02:37View SolutionSum of products P,Q,R,S (i.e. P+Q+R+S) is equal to:
02:07View SolutionWrite the following sentence in symbolic form. Sum of cubes of p and q is equal to thrice the product of r and s.
04:09View SolutionFrame the formula for the sentence given below. The sum of the cube of p and the product of 8 and q is equal to the sum of the product of 21, s and the product of 4 and the square of r.
07:23View SolutionP और Q भाई है । R और S बहनें है । P का पुत्र S का भाई है । Q का R से क्या संबंध है ?
09:27View SolutionP का भार Q का दोगुना है Q का भार R का आधा है R का भार T का 3 गुना है | T का भार S का आधा है क्यू का भार ,P , Q , R तथा S में से कितने व्यकितयों से अधिक है ?
View Solutionएक समांतर श्रेढ़ी में , Sp=q,sq=P तथा इसके प्रथम r - पदों का योगफल S _(r ) है तो Sp+q=
06:10View SolutionIf S be the sum, P the product and R the sum of the reciprocal of n terms in G.P., prove that, p2=(SR)n.
06:56View SolutionIf sum of the n terms of a G.P be S, their product P and the sum of their reciprocals R, then prove that P2=(SR)n
04:13View Solutionযদি কোনাে গুণােত্তর শ্রেণির পরপর n -সংখ্যক পদের যােগফল S , গুণফল P এবং পদগুলির অন্যান্যকের যােগফল R হয় , তবে প্রমাণ করাে যে , P2=(SR)n ।
01:26View SolutionIf S is the sum, P the product and R the sum of the reciprocals of n terms in G.P., prove that P2=(SR)n .
02:37View SolutionIf S be the sum. P be the product,and R the sum of the reciprocals of n terms in a G.P., Prove thatP2=(SR)n
09:19View Solution