Question

A car starts from rest on a half kilometer long bridge. The coefficiet of friction between the tyre and the road is 1.0. Show that one cannot drive thrugh the bridge in less than 10 s.

Explanation

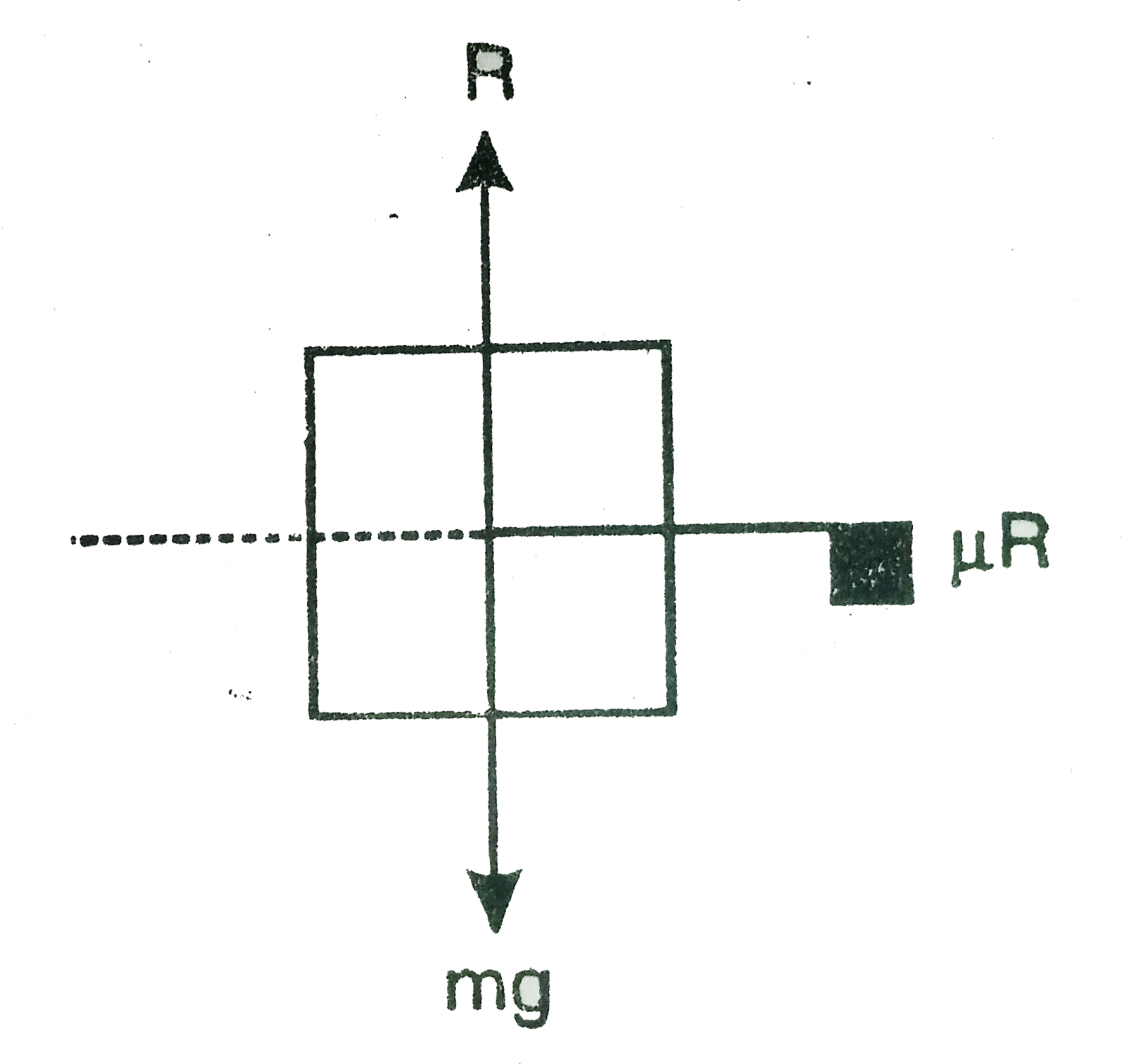
Let a maximum acceleratin is produced in car
`ma-mu R`
(for more accelerations the tyres will slip)
`rarr ma =mu mg`
`rarr a=mu g=1xx10=10 m/s^2` Force crossing of the bridge in minimum time, it has to travel with maximum acceeleration.
u=0, S=500m, a=10m/s
`From S=ut+1/2 at^2`
`500=0+(1/2)10t^2`
`rarr t=sqrt100=10sec`

If acceleration is less than `10 m/s^2` timewill be more than 10 sec. So one can't drive throughthe bridge in less than 10 s.