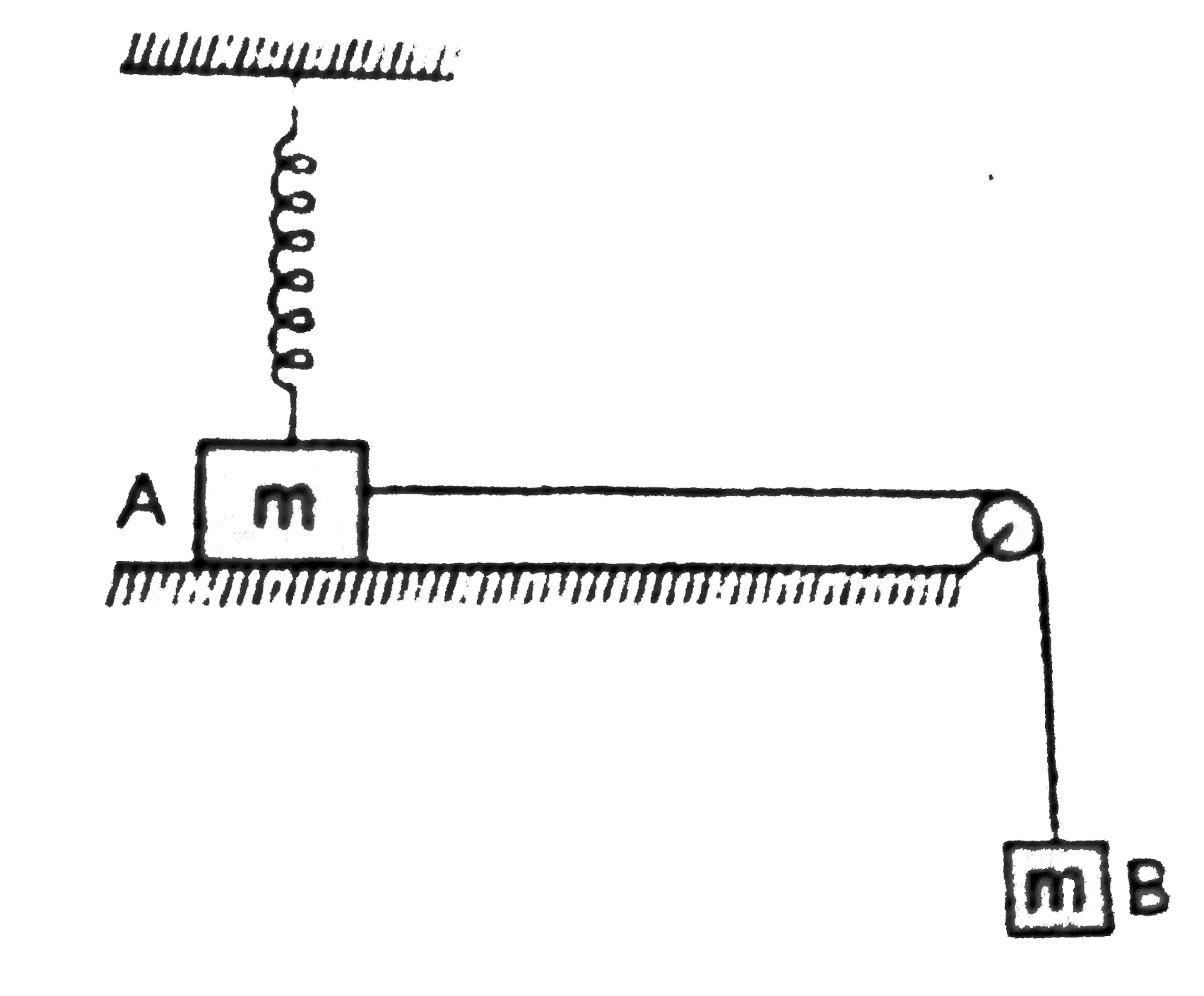
Figure shows two block A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to spring constant 40N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g=10m/s2 .
 Solution in Tamil
Solution in Tamil
The correct Answer is:A
m=320g=0.32kg,k=40Nm
h=40cm=0.4m,g=10msec2
From the free body diagram,
kxcosθ=mg
(when the block breaks of R=0)<br>rarr costheta=(mg)/(kx)<br>rarr 0.4/(0.4+x=3.2/(40x)<br>rarr 16x=3.2x+1.28<br>rarr x=0.1m<br>So,s=AB=sqrt((h+x^2)-h^2)<br>=sqrt((0.5)^2-(0.4)^2)=0.3m
Let the velocity of tebody at B be v change in K.E. work done (for the system)
(12μ2+12mv2)=−12kx2+mgs
→(0.32)×v2
=−(12)×40×(1.0)2+(0.2)×10×(0.3)
→v=1.5msec
Fromtheure<br>/_\l=h(sectheta-1)........i<br>Fromthee≠rgyconservation<br>mgs=2[1/2mv^2]+1/2K/_\l^2<br> mgh than theta =mv^2+1/2kh^2(sectheta-1)^2.....ii<br>Fromthelawofmotionatbreakof<br>mgkh(sectheta-1)costheta<br>rarr 1-costheta=mg/kh<br>rarr costheta=1-mg/kh<br>or costheta=(kh-mg)/kh<br>orcostheta=(kh-mg)/kh<br>=(40xx0.4-0.32xx10)/(40xx0.4)<br>=0.8<br>Pu∈gthevalueoftheta∈equationi,<br>0.32xx10xx0.4xx0.75<br>=0.32v^2+1/240xx(0.4)^2(1.25-1)^2<br>rarr 0.96=0.32v^2+0.2<br>rarr 0.32v2=0.72
rarr v=1.5m/sec
Topper's Solved these Questions
Similar Questions
A heavy stone is thrown from a cliff of height h with a speed v. The stone will hit the ground with maximum speed if it is thrown
View SolutionA wave pulse passing on a string with speed of 40cms−1 in the negative x direction has its maximum at x=0 at t=0. Where will this maximum be located at t=5s?
View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)

View SolutionTwo blocks A and B are connected to each other by a string and a spring, the string passes over a frictionless pulley as shown in Block B slides over the horizontal surface of a stationary block C and the block. A slides along the vertical side of C, both with same uniform speed. The coefficient of friction between the surface of the blocks is 0.2 Force constant of the spring is 1960 N/m if the mass of block A is 2 kg calculate the mass of the block B and the energy stored in the spring.
View Solutionचित्र में दो गुटके A एंव B दिखाए गए हैं । जिनमें प्रत्येक का द्रव्यमान 320g हैं । इनको एक घिरनी से गुजरनेवाली नगण्य भार वाली डोरी से जोड़ा गया हैं । गुटके A तथा इसके नीचे की क्षैतिज सतह के बीच घर्षण नगण्य हैं । गुटका A एक स्प्रिंग से जुड़ा हुआ हैं , जिसका स्प्रिंग नियतांक 40 N/m हैं तथा इस स्प्रिंग का दूसरा सिरा क्षैतिज सतह से 40 cm ऊपर जड़ा हुआ ( fixed) हैं । प्रारंभ में स्प्रिंग ऊर्ध्वाधर हैं तथा अपनी स्वाभाविक लंबाई में हैं । अब गुटके B को गिरने के लिए छोड़ दिया जाता हैं

View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
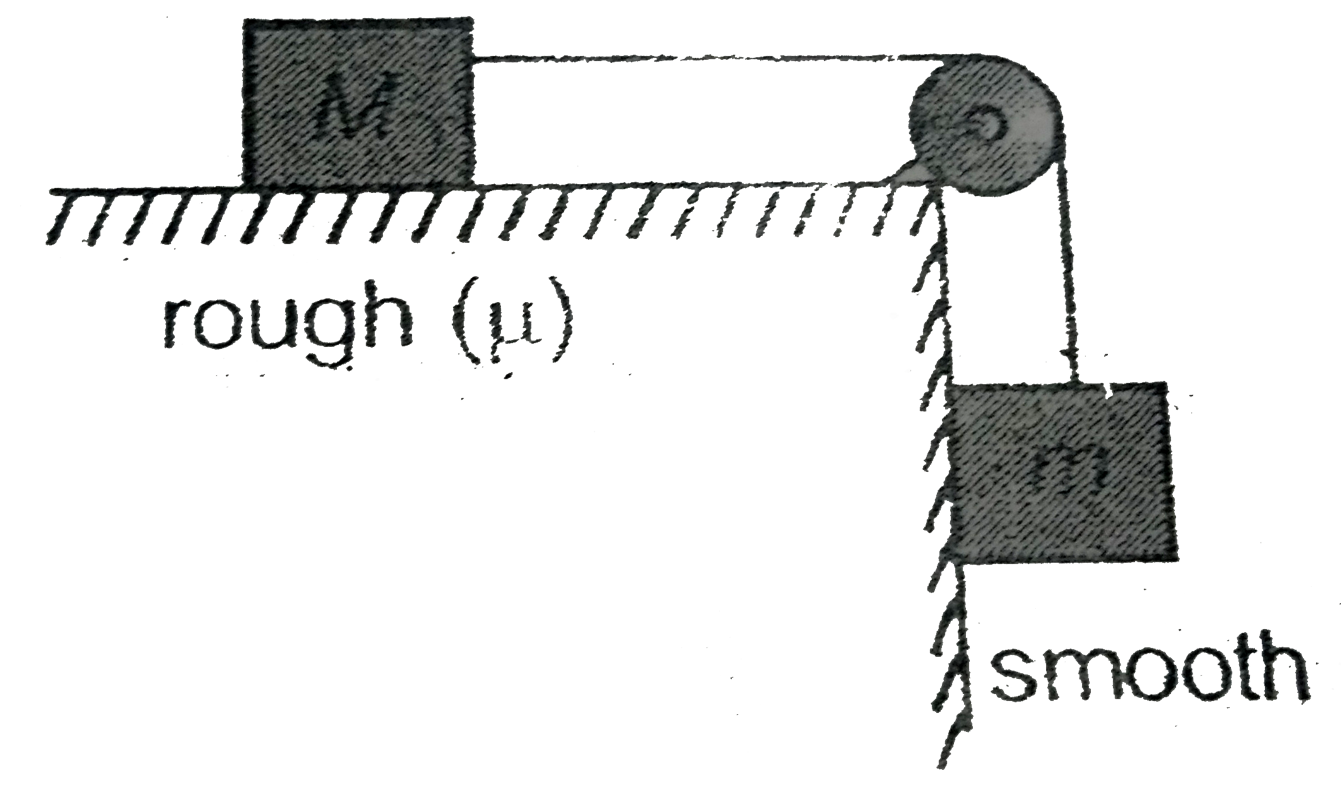
If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface is
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
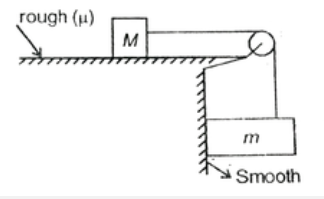
The minimum value of coefficient of friction μ such that system remains at rest , is
View SolutionFigure shows two block A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to spring constant 40N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g=10m/s2 .

View SolutionIn the shown figure mass of the pulley is m and radius 2R. A light concentric spool of radius R is rigidly attached with the pulley. Two blocks A and B having masses m & 4m respectively are attached with the pulley by means of light strings. Lower surface of the block B is attached to a spring of stiffness ka and block B rests on a smooth inclined plane inclined 30∘ with horizontal. Other end of the spring is fixed to the ground. The block A is stretched a small distance and released then find the frequency of the oscillation of block B. (The strings do not slip on the pulley).

View SolutionA block of mass m sliding on a smooth horizontal surface with a velocity →V meets a long horizontal spring fixed at one end and having spring constant k as shown in figure. Find the maximum compression of the spring?

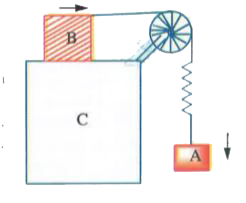
View SolutionTwo blocks A and B are connected to each other by a string and a spring, the string passes over a frictionless pulley as shwon in figure. Block B slides over the horizontal top surface of a stationary block C and block A slides along the vertical side of C, both with the same uniform speed. The coefficient of friction between the surfaces of blocks is 0.2. Force constant of the spring is 1960 N/m. If mass of block A is 2 kg calculate the mass of block B and the energy stored in the spring.
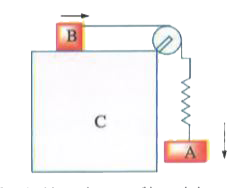
View SolutionTwo blocks A and B are connected to each other by a string and a spring. The string passesover a frictionless pulley as shown in the figure. Block B slides over the horizontal top surface of a stationary block C and the block A slides along the vertical side of C, both with the same uniform speed.
The coefficient of friction between the surfaces of blocks is 0.2. Force constant of the spring is 1960 N/m. If mass of block A is 2 kg. Calculate the mass of block B and the energy stored in the spring.
View SolutionA block of mass 'm' is attached to one end of a light inextensible string passing over a smooth light Pulley B and under another smooth light Pulley A as shown is figure. The other end of a string is fixed to a ceilling . A and B are held by springs of spring constant K_1 and K_2 . Find the angular frequency of small oscillation of the system
View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)
View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
View SolutionTwo blocks A and B of mass 16kg and 64kg are placed on a smooth horizontal surface. Blocks are connected by a spring of spring constant 100 N//m . Find the ratio of maximum speed of block A to maximum speed of block B .
View Solution
