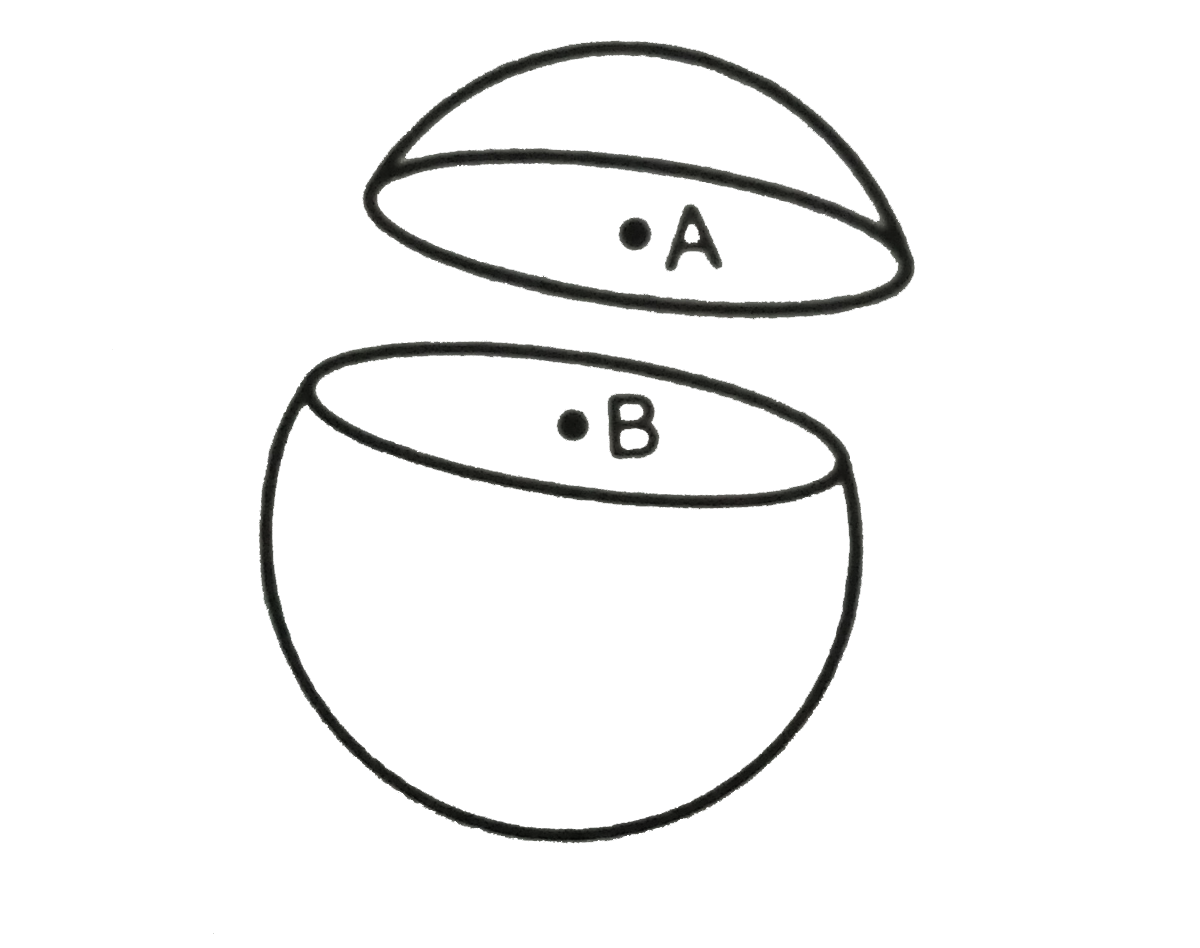
A thin sphereical shell having uniform density is cut in two parts by as plane and kept separated as shown in figure. The point A is the center of the plane section of the first part and B is the center of the plane section of the second part. Show that the gravitational field at A due to the first part is equal in magnitude to the gravitational field at B due to the second part.
Solution in Tamil
The correct Answer is:A
We know in the thin sphereical shell of uniform density has gravitatioiN/Asl field at its interN/Al point is zero at A and B points, field is equal and opposite and canel each other. So Net field is zero.
Hence, EA=EB
Topper's Solved these Questions
Similar Questions
The gravitational potential at a point due to a point mass is V=
01:07View SolutionA body slipping on a rough horizontal plane moves wioth a deceleationof 4.0ms. What is cofficient of kineic friction between the block and the plane?
15:21View SolutionThe steam point and the ice point of a mercury thermometer are marked as 80∘C and 20∘C. What will be the temperature in centigrade mercury scale when this thermometer reads 32∘C?
02:50View SolutionA spherical shell is cut into two pieces along a chord as shown in the figure. P is a point on the plane of the chord. The gravitational field at P due to the upper part is I1, and that due to the lower part is I2. What is the relation between them?
04:10View SolutionABCDA is a closed loop of conducting wire consisting of two semicircular sections, the part ABCD lying in the XY plane and the part CDA lying in the YZ plane, both the parts having the centre at origin O (see the diagram). This loop is placed in a uniform field vec(B) which varies with time. Radius of the semicircular section is 0.5 m If vec(B) be directed along the +z axis and increases at the rate of 10^(-2) ("Tesla")/("second") . the magnitude and sense of the induced emf in the loop as seen along the field direction will be
03:02View SolutionA small section of area ΔA is removed from a uniform spherical shell with surface mass density σ and radius R as shown in the figure . Find the magnitude of gravitational field intensity at point P due to the remaining mass .
View SolutionFigure show a hemispherical shell having uniform mass density The direction of gravitational field at point P will be along
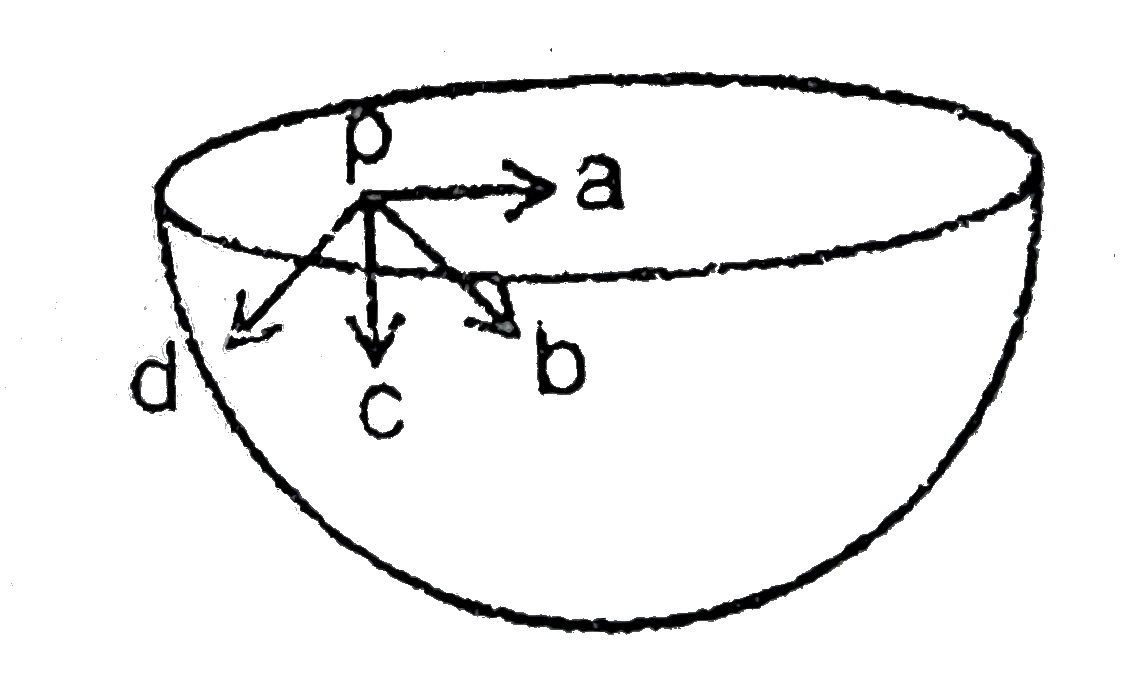.02:18View Solutionएक पतला एवं समरूप घनत्व वाला गोलीय कोश एक समतल द्वारा दो भागों में काटकर चित्रानुसार रखा गया है। प्रथम भाग के समतल काट का केद्र A तथा द्धितीय भाग के समतल काट का केद्र B है। दिखाऍं कि प्रथम भाग के कारण बिंदु A पर गुरूत्वीय क्षेत्र का परिमाण द्धितीय भाग के कारण बिंदु B पर क्षेत्र के परिमाण के बराबर होगा।
View SolutionA thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is
03:30View SolutionIf gravitational field due to uniform thin hemispherical shell at point P is I, then the magnitude of gravitational field at Q is (Mass of hemispherical shell is M, radius is R)
01:16View SolutionIf gravitational field due to a uniform thin hemispherical shell at point P (see figure) is I, then find the magnitude of gravitational field at Q (Mass of hemispherical shell is M, radius R)
04:15View SolutionIn two parts (sections) of a circular loop, an equal current is flowing as pictured. The radius of the loop is r. The magnitude on the magnetic field at the center of the loop is
03:42View SolutionA spherical shell is cut into two pieces along a chord as shown in the figure. P is a point on the plane of the chord. The gravitational field at P due to the upper part is I1, and that due to the lower part is I2. What is the relation between them?
01:32View SolutionA thin conducting ring of radius R is given a charge +Q , Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E . The electric field at the center due to the charge on part ACDB of the ring is
01:41View SolutionA small section of area DeltaA is removed from a uniform spherical shell with surface mass density sigma and radius R as shown in the figure . Find the magnitude of gravitational field intensity at point P due to the remaining mass .
04:32View SolutionIf a wire of uniform cross sectional area is cut equally into two parts the resistivity part
01:38View Solution