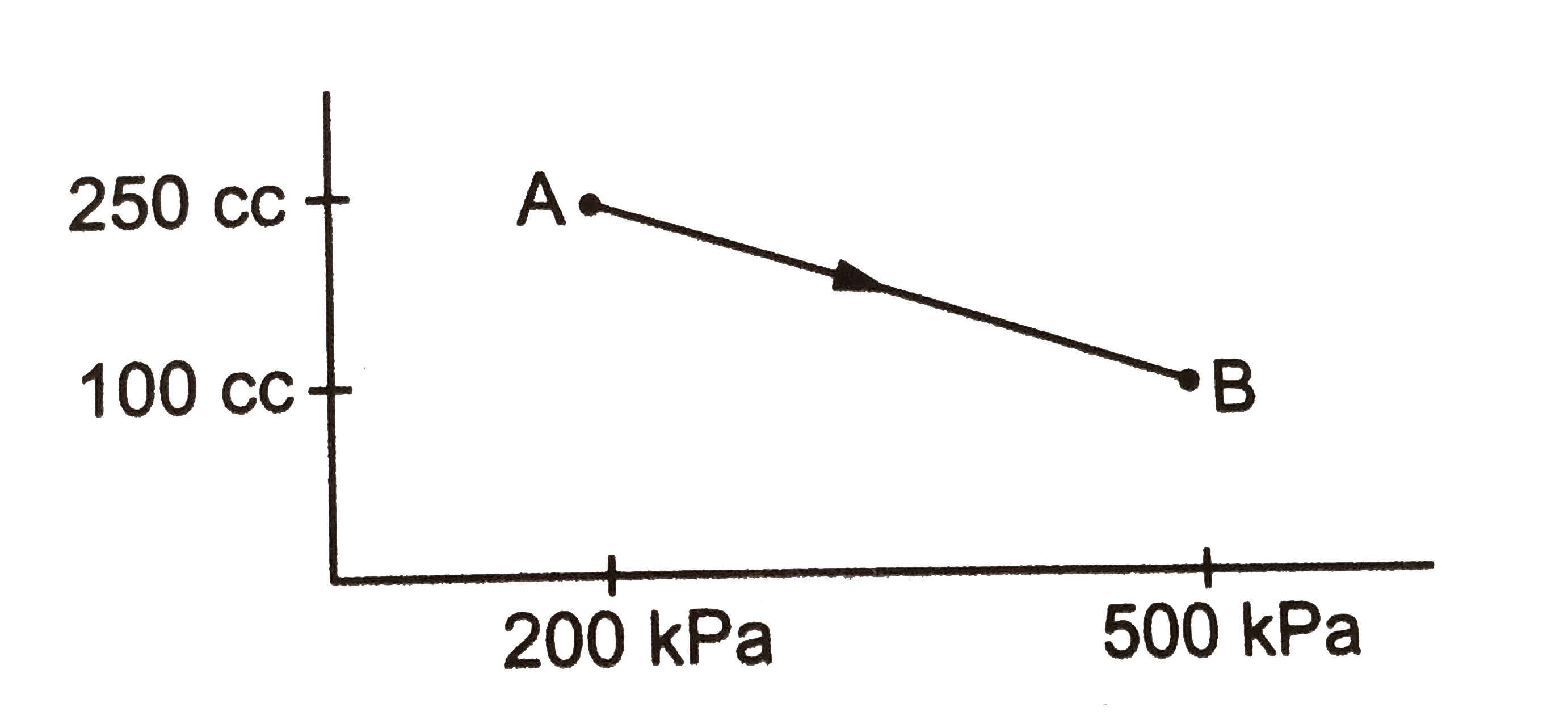
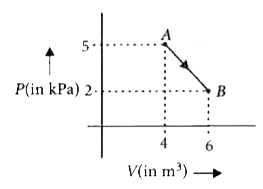
A gas is taken along the path AB as shown in fig, if 70 cal of heat is extracted from the gas in the process, calculate the change in the internal energy of the system.
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B, D
Delta Q = 70cal = (70xx4.2)J<br>Delta W = (1)/(2)xx(200+500)xx10^3xx150xx10^(-6)<br> = (1)/(2)xx700xx150xx10^(-3)<br> = 525xx10^(-1) = 52.5J<br>Delta U = ?<br>DeltaQ = DeltaU+Delta W<br>rArr -294 = Delta U+52.5<br>rArr Delta U = -294-52.5 = -346.5J
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
14 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Objective II
5 Videos
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - All Questions
120 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
Similar Questions
Should the internal energy of a system necessarily increase if heat is added to it?
View SolutionThe pressure p and volume V of an ideal gas both increase in a process.
View SolutionCalculate the rms speed of nitrogen at STP (pressure =1 atm and temperature =00C. The density of nitrgoen in these conditions is 1.25kgm−3
View SolutionA block of mass 2 kg placed on a long frictionless horizontal table is pulled horizontally by a constant foerce F. It is found to move 10 m in the first two seconds. Find the magnitude of F.
View Solution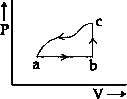
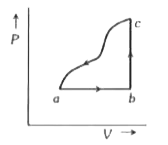
A sample of an ideal gas is taken through the cyclic process abca and shown in the figure. The chagne in the internal energy of the gas along the path ca is −180J. The gas aborbs 250J of heat along the path ab and 60 J along the path bc. the work done by the along the path abc is:
View SolutionIn following figs. Variation of volume by change of pressure is shown in Fig. A gas is taken along the path ABCDA . The change in internal energy of the tgas will be:
View SolutionA mono-atomic gas is taken along path AB as shown. Calculate change in internal energy of the gas.
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure, The change in internal energy of the gas during the transition is :
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure

The change to internal energy of the gas during the transition is
View Solutionएक आदर्श गैस को, चित्र में दर्शाये गये अनुसार चक्रीय प्रक्रम abca से गुजारा जाता है। ca पथ के अनुदिश गैस की आन्तरिक ऊर्जा में परिवर्तन -180 J है। ab पथ के अनुदिश, गैस 250 J ऊष्मा अवशोषित करती है तथा bc पथ के अनुदिश, गैस 60 J ऊष्मा अवशोषित करती है तो. पथ abc के अनुदिश, गैस द्वारा किया गया कार्य है
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure. The change in internal energy of the gas during the transition is
View Solutionएक आदर्श गैस को, चित्र में दर्शाये गये अनुसार चक्रीय प्रक्रम abca से गुजारा जाता है। ca पथ के अनुदिश गैस की आन्तरिक ऊर्जा में परिवर्तन -180 J है। ab पथ के अनुदिश, गैस 250 J ऊष्मा अवशोषित करती है तथा bc पथ के अनुदिश, गैस 60 J ऊष्मा अवशोषित करती है तो. पथ abc के अनुदिश, गैस द्वारा किया गया कार्य है

View SolutionIn following figs. Variation of volume by change of pressure is shown in Fig. A gas is taken along the path ABCDA . The change in internal energy of the gas will be:
View SolutionA sample of an ideal gas is taken through the cyclic process abca and shown in the figure. The change in the internal energy of the gas along the path ca is -180J . The gas absorbs 250J of heat along the path ab and 60 J along the path bc. the work done by the gas along the path abc is:
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A and B along a path AB as shown in the figure The change in internal energy of the gas during the transition is
View SolutionChoose the correct option: In following figs. Variation of volume by change of pressure is shown in Fig. A gas is taken along the path ABCDA . The change in internal energy of the the gas will be:
View Solution
