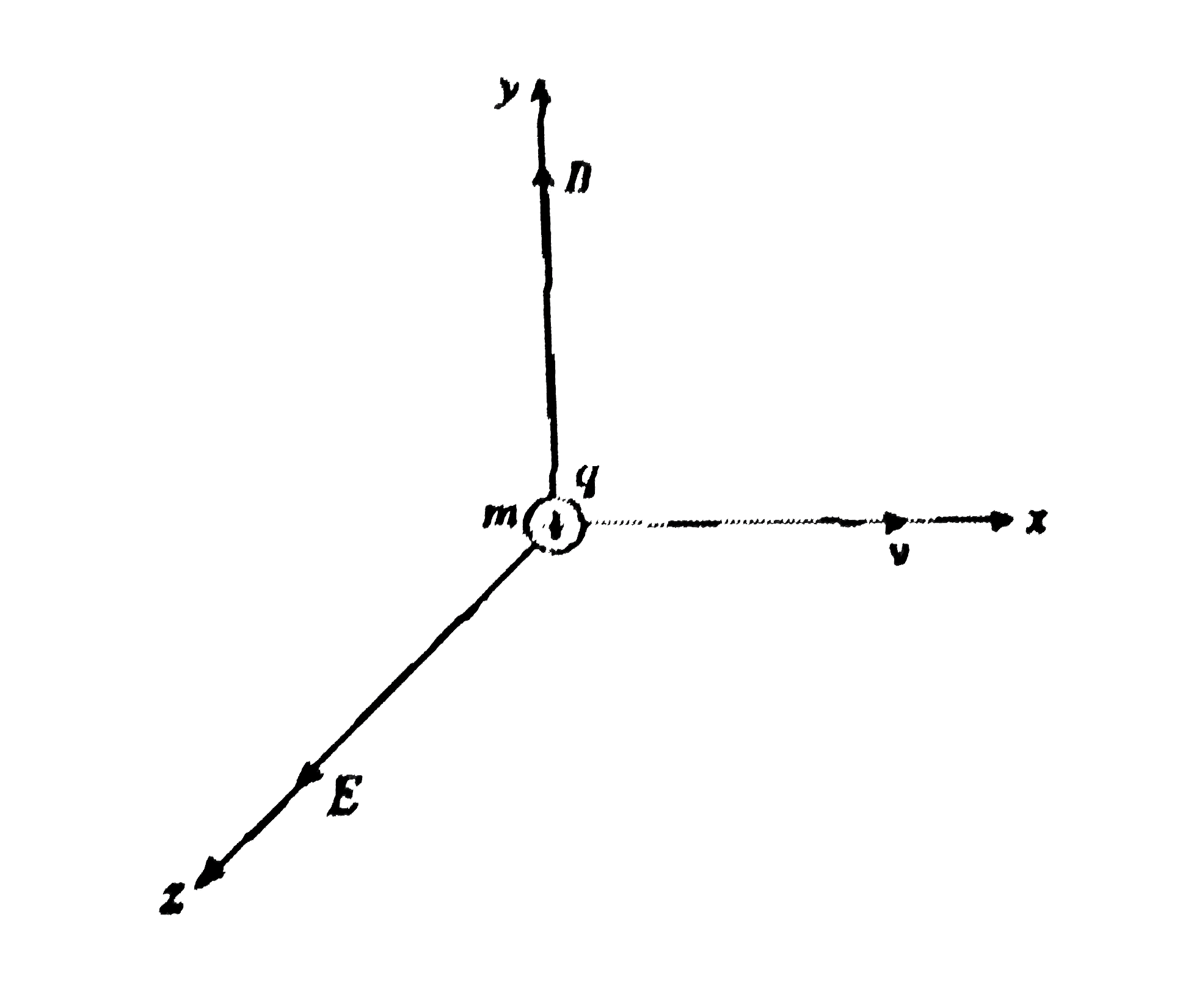
A particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are given by
→B=−B0→Jand→E−E0→K.
Find the speed of the particle as a function of its z-coordinate.Solution in Tamil
Velocity will be along x−zpla≠−¯¯¯B
=−¯¯¯B0¯¯¯J,¯¯¯E=E0¯¯¯¯K
F=q(E+V×B)
=qE0K−qVxB0K+qVxB0I
SinceVx=0,F2=qE0
so a=qE0m
∴V2=u2+2as=2qE0□mz
so,v=√2qE0zm
[dist along z - direction be z ].
Topper's Solved these Questions
Similar Questions
If a charged particle at rest experiences no electromagnetic force, then electric field in that region
View SolutionFind the range of frequency of light that is visible to an average human being (400nm<λ<700nm)
View SolutionUsing the formulae ((→F)=(→qv)×(→B)andB=(μ0)i2πr,find the SI units of the magnetic field B and the permeability constant
View SolutionA charged particle of mass m and charge q is released from rest the position (x_0,0) in a uniform electric field E_0hatj . The angular momentum of the particle about origin.
View SolutionA particle having mass m and charge q is released from the origin in a region in which ele field and magnetic field are given by B=−B0ˆjand E=E0ˆk.
Find the y- component of the velocity and the speed of the particle as a function of it z-coordinate.
View SolutionA charged particle moving with a uniform velocity →v enters a region where uniform electric and magnetic fields →E and →B are present. It passes through the region without any change in its velocity. What can we conclude about the (i) relative direction of →E, →V and →B? (ii) magnetic of →E and →B?
or
Find the condition under which the charged particle moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speeds.
View SolutionA charged particle of charge e and mass m is moving in an electric field →E and magnetic field →B. Constant dimensionless quantities and quantities of dimention [T]−1.
View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and megnetic field are given by →B=−B0ˆj and →E=→E0ˆk. Find the speed of the particle as a function of its z-coordinate.
View SolutionA particle of mass m and charge q is thrown from origin at t=0 with velocity 2hati+3hatj+4hatk units in a region with uniform magnetic field vecB=2hati units. After time t=pim//qB , an electric field vecE is switched on such that particle moves on a straight line with constnat speed vecE may be:
View SolutionA charge particle of charge q, mass m is projected with a velocity →v=vˆi in a region of space where electric field strength →E=Eˆk and magnetic induction →B=Bˆj are present. The acceleration of the particle is:
View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are ginen by B=+B_(0)hatj and vecE=+E_(0)hati . Find the speed of the particle as a function of its X -coordinate.
View SolutionA charged particle of charge e and mass m is moving in an electric field vecE and magnetic field vecB . Construct dimensionless quantities and quantities of dimension [T]^(-1) .
View SolutionA charged particle of charge e and mass m is moving in an electric field →E and magnetic field →B. Construct dimensionless quantities and quantities of dimention [T]−1.
View SolutionA particle of charge q, mass starts moving from origin under the action of an electric field →E=E0ˆi and magnetic field →B=B0ˆk . Its velocity at (x,0,0) is v0(6ˆi+8ˆj). The value of is
View SolutionA particle having charge q moves with a velocity v through a region in which both an electric field →E and a magnetic field B are present. The force on the particle is
View SolutionElectric field and magnetic field in a region of space are given by(Ē= E_0 hat j). and (¯¯¯B=B0ˆj). A charge particle is released at origin with velocity (¯v=v0ˆk) then path of particle is
View Solution